Exercise

Prove that $2\sqrt{3}+\sqrt{5}$ is irrational.

Let $p$ be a prime number. If $p$ divides $a^2$ (where $a$ is a positive integer), then $p$ divides $a$. Verify the statement for $p=2, p=5$ and for $a^2=1, 4, 9, 16, 25, 36, 49, 64, 81$ 

Parul and Nupur both study in class $\mathrm{X}$. Today, they were taught about the Fundamental Theorem of Arithmetic which states that, "Every composite number can be expressed (factorised) as a product of primes, and this factorisation is unique, apart from the order in which the prime factors occur".

To explain the Fundamental Theorem of Arithmetic, their teacher recalled the prime factorisation of a number by the 'factor tree method'. 

Parul became interested in the factor tree method and she asked Nupur to help to complete the following factor tree.

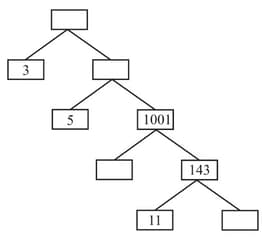
Find the missing numbers.

Solve $\frac{\sqrt{2}\left(2+\sqrt{3}\right)}{\sqrt{3}\left(\sqrt{3}+1\right)}-\frac{\sqrt{2}\left(2-\sqrt{3}\right)}{\sqrt{3}\left(\sqrt{3}-1\right)}$

If $x=\frac{\sqrt{3}+1}{\sqrt{3}-1}$ and $y=\frac{\sqrt{3}-1}{\sqrt{3}+1}$ then prove that $\frac{x^2+y^2}{x^2-y^2}=\frac{7\sqrt{3}}{12}$.

Let $p$ be a prime number and $k$ be a positive integer. If $p$ divides $k^2$, then which of these is definitely divisible by $p$?

$\sqrt{n}$ is a natural number such that $n>1$. Which of these can definitely be expressed as a product of primes.

$i) \sqrt{n}$

$ii)\hspace{0.17em}n$

$iii)\hspace{0.17em}\frac{\sqrt{n}}{2}$

Prove that $\sqrt{p}+\sqrt{q}$ is an irrational, where $p, q$ are primes.