NCERT Solutions for Chapter: Circles, Exercise 4: Exercise
NCERT Mathematics Solutions for Exercise - NCERT Solutions for Chapter: Circles, Exercise 4: Exercise
Attempt the free practice questions on Chapter 10: Circles, Exercise 4: Exercise with hints and solutions to strengthen your understanding. NCERT Exemplar Mathematics - Class 9 solutions are prepared by Experienced Embibe Experts.
Questions from NCERT Solutions for Chapter: Circles, Exercise 4: Exercise with Hints & Solutions
If is an equilateral triangle inscribed in a circle and be any point on a minor which does not coincide with or , prove that is angle bisector of .
In the given fig., and are two chords of a circle intersecting each other at point . Prove that (Angles subtended by an at the centre angle subtended by arc at the centre.)
If bisectors of opposite angles of a cyclic quadrilateral intersect the circle, circumscribing it at the points and , prove that is a diameter of the circle.
A circle has radius It is divided into two segments by a chord of length
Prove that the angle subtended by the chord at a point in major segment is .
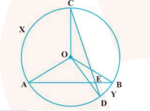
Two equal chords and of a circle when produced intersect at a point . Prove that .
and are two chords of a circle of radius such that . If and are the distances of and from the centre, prove that .
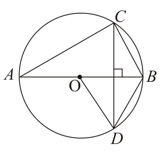
In Fig. , is the centre of the circle, . Find and .
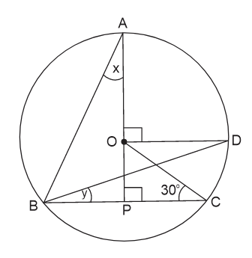
is the centre of the circle, and . If , then find the value of