B M Sharma Solutions for Chapter: Linear and Angular Simple Harmonic Motion, Exercise 2: CONCEPT APPLICATION EXERCISE

A body performs simple harmonic oscillations along the straight line $PQRST$ with $R$ as the midpoint of $PT.$ Its kinetic energies at $Q$ and $S$ are each one fourth of its maximum value. If $PT=2 A,$ find the distance between $Q$ and $S.$

The potential energy between two atoms in a diatomic molecule varies with $x$ as $U=\frac{a}{x^{12}}-\frac{b}{x^6},$ where $a$ and $b$ are positive constants. Find the equivalent spring constant for the oscillation of one atom if the other atom is kept stationary.

(i) The acceleration versus time graph of a particle executing SHM is shown in the following figure. Plot the displacement versus time graph.

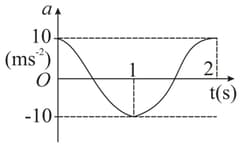
(ii) The frequency of oscillation is __________.

(iii) The displacement amplitude is ______.

(iv) At $t=0$, the velocity of the particle is ______/

(v) The kinetic energy of the particle is maximum at $t=$_____ and $t=$______.

(vi) The potential energy is maximum at $t=$ _______; $t=$_______ and $t=$_______.

A particle starts oscillating simple harmonically with time period $T$ from its equilibrium position. Find the ratio of kinetic energy and potential energy of the particle at the time $\frac{T}{12}.$ ($T=$time period).

The potential energy of a simple harmonic oscillator of mass $2 \mathrm{kg}$ in its mean position is $5 \mathrm{J}.$ If its total energy is $9 \mathrm{J}$ and its amplitude is $0.01 \mathrm{m},$ find its time period.

If you start measuring the time from the mean position, after what minimum time the energy of a horizontal spring mass system oscillating with time period $T$ is half kinetic and half potential?

A linear harmonic oscillator has a total mechanical energy of $200\mathrm{J}$. Potential energy of it at mean position is $50\mathrm{J}$. Find

(i) The maximum kinetic energy

(ii) The minimum potential energy

(iii) The potential energy at extreme positions.

The potential energy of a particle oscillating on $x-$axis is given as $U=20+{\left(x-2\right)}^2$.

Here $U$ is in joules and $x$ in metres. Total mechanical energy of the particle is $36\mathrm{J}$.

(a) State whether the motion of the particle is simple harmonic or not.

(b) Find the mean positive

(c) Find the maximum kinetic energy of the particle.