B M Sharma Solutions for Chapter: Linear and Angular Simple Harmonic Motion, Exercise 2: CONCEPT APPLICATION EXERCISE

A block of mass $m$ is suspended from the ceiling of a stationary elevator through a spring of spring constant $k$; it is in equilibrium. Suddenly, the cable breaks and the elevator starts falling freely. Show that the block now executes a simple harmonic motion of amplitude $\frac{mg}{k}$ in the elevator.

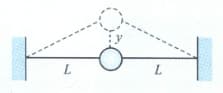
A ball of mass $m$ is connected to two rubber bands of length $L$, each under tension $T$ as shown in the figure. The ball is displaced by a small distance $y$ perpendicular to the length of the rubber bands. Assuming the tension does not change, show that

(a) the restoring force is $-\left(\frac{2\mathrm{T}}{L}\right)y$ and

(b) the system exhibits simple harmonic motion with an angular frequency $\omega =\sqrt{\frac{2\mathrm{T}}{mL}}$.

A mass $M$ attached to a spring oscillates with a period of $2\mathrm{s}$. If the mass is increased by $2\mathrm{kg}$, the period increases by $1\mathrm{s}$, find the initial mass $M$ assuming that Hooke's law is obeyed.

A spring of spring constant $200{\mathrm{Nm}}^{-1}$ has a block of mass $1\mathrm{kg}$ hanging at its one end and from the other end the spring is attached to a ceiling of an elevator. The elevator rises upwards with an acceleration of $\frac{g}{3}$. When acceleration is suddenly ceased, then what should be the angular frequency and elongation during the time when the elevator is accelerating?

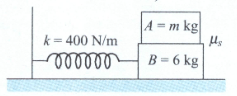
Two blocks lie on each other and are connected to a spring as shown in the figure. What should be the mass of block $A$ placed on block $B$ of mass $6\mathrm{kg}$ so that the system is period is $1\mathrm{s}$. Assuming no slipping, what should be the minimum value of coefficient of static friction $\mu$, for which block $A$ will not slip relative to block $B$, if block $B$ is displaced $50\mathrm{mm}$ from equilibrium position and released?

(Given: $g=10{\mathrm{ms}}^{-2}$ and ${\pi }^2=10$)

A body is in SHM with period $T$ when oscillated from a freely suspended spring. If this spring is cut in two parts of length ratio $1:3$ and again oscillated from the two parts separately, then the periods are $T_1$ and $T_2$. Find $\frac{T_1}{T_2}$.

In the figure shown, the block $A$ of mass $M$ collides with the identical block $B$ and after collision they stick together. Calculate the amplitude of resultant vibration.

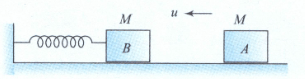
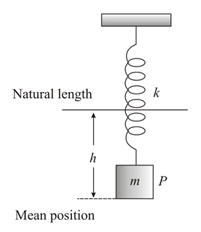
Figure shows a spring block system hanging in equilibrium. If a velocity $v_0$ is imparted to the block in downward direction, find the amplitude of SHM of the block and the time after which it will reach a point at half of the amplitude of block.