B M Sharma Solutions for Chapter: Kinematics II, Exercise 76: CONCEPT APPLICATION EXERCISE 5.5

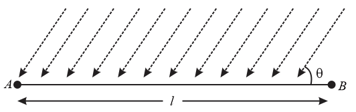
An aeroplane flies along a straight path $A$ to $B$ returns back again. The distance between $A$ and $B$ is $l$ and the aeroplane maintains the constant speed $v$ with respect to the wind. There is a steady wind with a speed $u$ at an angle $\theta$ with line $AB$. Determine the expression for the total time of the trip.

A pilot is supposed to fly a certain distance $AB$, due east from $A$ to $B$ and then due west from $B$ to $A$. The velocity of plane is $v$ and that of air is $u$. The time for the round trip is $t_0$ in still air. Show that

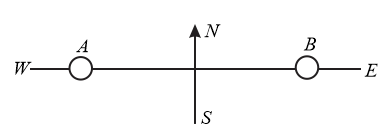
(a) If the air velocity be due east or west, the time for the round trip will be $t_1=\frac{t_0}{\left(1-{\displaystyle \frac{u^2}{v^2}}\right)}$

(b) if the air velocity is due north or south, the time for a round trip will be $t_2=\frac{t_0}{\sqrt{\left(1-\frac{u^2}{v^2}\right)}}.$

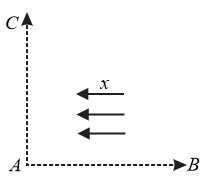
Wind blows with a velocity $x$ in the direction shown in the figure. Two aeroplanes start out from point $A$ and fly with a constant speed $y$. The first flies from $A$ to $C$. Both of them return to $A$. If $AB=AC$, which plane will return to point $A$ first, and what will be the ratio of the times of flight of the two planes?

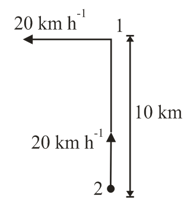
Two ships are $10 \mathrm{km}$ apart on a line joining south to north. The one farther north is streaming west at $20 \mathrm{km} {\mathrm{h}}^{-1}$. The other is streaming north at $20 \mathrm{km} {\mathrm{h}}^{-1}$. What is their distance of the closest approach? How long do they take to reach it?

A boatman finds that he can save $6 \mathrm{s}$ in crossing a river by the quickest path than by the shortest path. If the velocity of the boat and the river be, respectively, $17 \mathrm{m} {\mathrm{s}}^{-1}$ and $8 \mathrm{m} {\mathrm{s}}^{-1}$, find the river width.

A man directly crosses a river in time $t_1$ and swims down the current at a distance equal to the width of the river in time $t_2$. If $u$ and $v$ be the speed of the current and the man, respectively, show that $\frac{t_1}{t_2}:\frac{\sqrt{v+u}}{\sqrt{v-u}}$.

A person rows a boat across a river making an angle of $60°$ with the downstream. Find the percentage time he would have saved, had he crossed the river in the shortest possible time.

A person, intending to cross a river by the shortest path, starts at an angle $\alpha$ with the downstream. If the speed of the person is less than that of the water current, show that $\alpha$ must be obtuse.