B M Sharma Solutions for Chapter: Newton's Laws of Motion (Without Friction), Exercise 72: Exercises

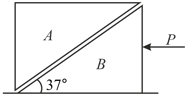
A small block of mass $m=2 \mathrm{kg}$ is kept at rest at the bottom of the inclined plane of a wedge of mass $M=9 \mathrm{kg}$. A force of $210 \mathrm{N}$ is applied on the wedge horizontally as shown in the diagram. All the surfaces are smooth. Determine the time taken in seconds by the mass $m$ to reach the highest point of the inclined plane of the wedge? $\left(g=10 \mathrm{m} {\mathrm{s}}^{-2}\right)$

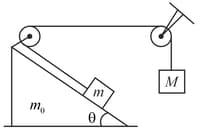
In the system shown in figure, all surfaces are smooth and string and pulleys are light. Angle of wedge $\mathrm{\theta }={\sin }^{-1}\left(\frac{3}{5}\right)$. When released from rest, it was found that the wedge of mass $m_0$ does not move. Find $\frac{m}{M}$.

In the system shown in figure, the two springs $S_1$ and $S_2$ have force constant $k$ each. Pulley, springs and strings are all massless. Initially, the system is in equilibrium with spring $S_1$ stretched and $S_2$ relaxed. The end $A$ of the string is pulled down slowly through a distance $L=10 \mathrm{cm}$. By what distance (in $\mathrm{cm}$) does the block of mass $M$ move?

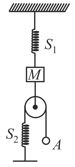
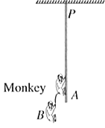
A monkey $A (\mathrm{mass}=6 \mathrm{kg})$ is climbing up a rope tied to a rigid support. The monkey $B (\mathrm{mass}=2 \mathrm{kg})$ is holding on the tail of monkey $A$. If the tail can tolerate a maximum tension of $30 \mathrm{N}$, what maximum force should monkey $A$ apply on the rope in order to carry monkey $B$ with it? $\left(g=10 \mathrm{m} {\mathrm{s}}^{-2}\right)$

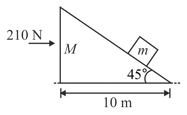
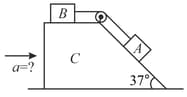
The upper surface of block $C$ is horizontal and its right part is inclined to the horizontal at angle $37°$. The mass of blocks $A$ and $B$ are $m_1=1.4 \mathrm{kg}$ and $m_2=5.5 \mathrm{kg}$, respectively. Neglect friction and mass of the pulley. Calculate acceleration $a$ with which block $C$ should be moved to the right so that $A$ and $B$ can remain stationary relative to it.

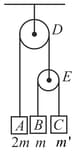
In the arrangement shown in figure, pulley $D$ and $E$ are small and frictionless. They do not rotate but threads slip over them without friction and their masses being $4 \mathrm{kg}$and $11.25 \mathrm{kg},$ respectively, while masses of block $A, B$ and $C$ are $2 m, m$ and $m\text{'}$, respectively. When the system is released from rest, downward accelerations of blocks $B$ and $C$ relative to $A$ are found to be $5 \mathrm{m} {\mathrm{s}}^{-2}$ and $3 \mathrm{m} {\mathrm{s}}^{-2}$, respectively.

Find the ratio of the acceleration of blocks $B$ and $C$, relative to the ground.

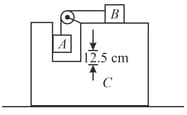
A small light pulley is attached with a block $C$ of mass $4 \mathrm{kg}$ as shown in the figure. Block $B$ of mass$1.5 \mathrm{kg}$ is placed on the top horizontal surface of $C$. Another block $A$ of mass $2 \mathrm{kg}$ is hanging from a string attached with $B$ and passing over the pulley. Taking $g=10 \mathrm{m} {\mathrm{s}}^{-2}$ and neglecting friction, find the acceleration of block $B$ (in $\mathrm{m} {\mathrm{s}}^{-2}$) when the system is released from rest.

Blocks $A$ and $B$ each have same mass $m=1 \mathrm{kg}$. Determine the largest horizontal force $P$ (in newton) which can be applied to $B$ so that $A$ will not slip up on $B$. Neglect any friction.