K A Tsokos Solutions for Chapter: Fields (HL), Exercise 2: Test yourself
K A Tsokos Physics Solutions for Exercise - K A Tsokos Solutions for Chapter: Fields (HL), Exercise 2: Test yourself
Attempt the practice questions on Chapter 10: Fields (HL), Exercise 2: Test yourself with hints and solutions to strengthen your understanding. Physics for the IB Diploma 6th Edition solutions are prepared by Experienced Embibe Experts.
Questions from K A Tsokos Solutions for Chapter: Fields (HL), Exercise 2: Test yourself with Hints & Solutions
Two stars of equal masses orbit a common mass as shown in the diagram. The radius of orbit of each star is . Assume that each star has a mass equal to (solar mass= ) and the initial separation of the star is .
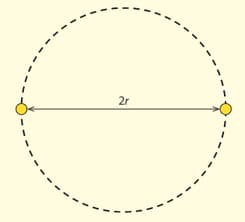
. The orbital period decreases at a rate of The two stars will collapse into each other when . Estimate the lifetime, in years of this binary star system
A charge whose mass moves in a circle of radius around another positive charge located at the centre of the circle, as shown in the diagram.
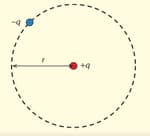
Draw the force on the moving charge.
A charge whose mass moves in a circle of radius around another positive charge located at the centre of the circle, as shown in the diagram.
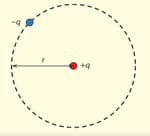
Show that the velocity of the charge is given by
A charge whose mass moves in a circle of radius around another positive charge located at the centre of the circle, as shown in the diagram.
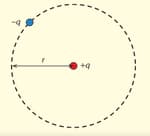
Show that the total energy of the charge is given by
A charge whose mass moves in a circle of radius around another positive charge located at the centre of the circle, as shown in the diagram.
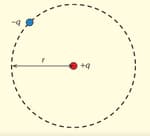
Show that the total energy of the charge is given by . Hence determine how much energy must be supplied to the charge if it is to be orbit around the stationary charge at a radius equal to .
An electron of charge and mass orbit the proton in a hydrogen atom. Show that the period of revolution of the electron is given by
where = Coulombs' constant. and = radius of the orbit.
An electron of charge and mass orbit the proton in a hydrogen atom. Show that the period of revolution of the electron is given by
where = Coulombs' constant. and = radius of the orbit.
Calculate this period for an orbit radius of
An electron of charge and mass orbit the proton in a hydrogen atom. Show that the period of revolution of the electron is given by
where = Coulombs' constant. and = radius of the orbit.
Using the results of the previous problem, calculate the energy that must be supplied to the electron so it orbits the proton in an orbit of
