Resnick & Halliday Solutions for Chapter: Motion in Two and Three Dimensions, Exercise 1: Problems

A train travels due south at $30 \mathrm{m} {\mathrm{s}}^{-1}$ ($1$ relative to the ground) in a rain that is blown towards the south by the wind. The path of each raindrop makes an angle of $70°$ with the vertical, as measured by an observer stationary on the ground on the ground. As an observer on the train, however, sees the drops fall perfectly vertically. Determine the speed of the raindrops relative to the ground.

A light plane attains an airspeed of $500 \mathrm{km} {\mathrm{h}}^{-1}$. The pilot sets out for a destination $900 \mathrm{km}$ due north but discovers that the plane must be headed $20.0°$ east of due north to fly there directly. The plane arrives in $2.00 \mathrm{h}$. What were the $\left(a\right)$ magnitude and $\left(b\right)$ direction of the wind velocity?

Snow is falling vertically at a constant speed of $8.0 \mathrm{m} {\mathrm{s}}^{-1}$. At what angle from the vertical do the snowflakes appear to be falling as viewed by the driver of a car traveling on a straight, level road with a speed of $50 \mathrm{km} {\mathrm{h}}^{-1}$?

In the overhead view of the figure, Jeeps $P$ and $B$ race along straight lines, across flat terrain, and past stationary border guard $A$. Relative to the guard. $B$ travels at a constant speed of $25.0 \mathrm{m} {\mathrm{s}}^{-1}$, at the angle ${\mathrm{\theta }}_2=30.0°$. Relative to the guard $P$ has accelerated from rest at a constant rate of $0.400 \mathrm{m} {\mathrm{s}}^{-2}$ at the angle ${\mathrm{\theta }}_1=60.0°$. At a certain time during the acceleration, $P$ has a speed of $40.0 \mathrm{m} {\mathrm{s}}^{-1}$. At that time, what are the $\left(a\right)$ magnitude and $\left(b\right)$ direction of the velocity of $P$ relative to $B$ and the $\left(c\right)$ magnitude and $\left(d\right)$ direction of the acceleration of $P$ relative to $B$?

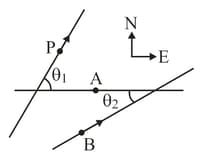
Two ships, $A$ and $B$ leave to the port at the same time. The ship $A$ travels northwest at $24 \mathrm{knots}$ and $B$ travels at $28 \mathrm{knots}$ in a direction $40°$ west of the south $\left(1 \mathrm{knot}=1 \mathrm{nautical} \mathrm{mile} \mathrm{per} \mathrm{hour}\right)$. What are the $\left(a\right)$ magnitude and $\left(b\right)$ direction of the velocity of the ship $A$ relative to $B$? $\left(c\right)$ After what time will the ship be $160 \mathrm{nautical} \mathrm{miles}$ apart? $\left(d\right)$ What will be the bearing of $B$ (the direction of $B$'s position) relative to $A$ at that time?

A $200 \mathrm{m}$ wide river flows due east at a uniform speed of $2.5 \mathrm{m} {\mathrm{s}}^{-1}$. A boat with a speed of $8.0 \mathrm{m} {\mathrm{s}}^{-1}$ relative to the water leaves the south bank pointed in a direction $30°$ west of north. What are the $\left(a\right)$ magnitude and $\left(b\right)$ direction of the boat's velocity relative to the ground? $\left(c\right)$ How long does the boat take to cross the river?

The ship, $A$ is located, $4.0 \mathrm{km}$ north and, $2.5 \mathrm{km}$ east of the ship, $B$. The ship, $A$ has a velocity of, $22 \mathrm{km} {\mathrm{h}}^{-1}$ towards the south, and the ship, $B$ has a velocity of, $40 \mathrm{km} {\mathrm{h}}^{-1}$ in a direction, $37°$ north of east. $\left(a\right)$ What is the velocity of $A$ relative to, $B$ in unit-vector notation with, $\hat{\mathrm{i}}$ towards the east? $\left(b\right)$ Write an expression (in terms of $\hat{\mathrm{i}}$ and $\hat{\mathrm{j}}$) for the position of $A$ relative to $B$ as a function of $t$, where $t=0$ when the ships are in the positions described above. $\left(c\right)$ At what time is the separation between the ships least? $\left(d\right)$ What is that least separation?

A $200 \mathrm{m}$ wide river has a uniform flow speed of  $1.1 \mathrm{m} {\mathrm{s}}^{-1}$ through a jungle and toward the east. An explorer wishes to leave a small clearing on the south bank and cross the river in a powerboat that moves at a constant speed of $5.0 \mathrm{m} {\mathrm{s}}^{-1}$ with respect to the water. There is a clearing on the north bank $82 \mathrm{m}$ upstream from a point directly opposite the clearing on the south bank. $\left(a\right)$ In what direction must the boat be pointed in order to travel in a straight line and land in the clearing on the north bank? $\left(b\right)$ How long will the boat take to cross the river and land in the clearing?