Resnick & Halliday Solutions for Chapter: Oscillations, Exercise 1: Problems

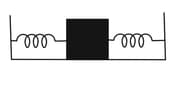
In the figure, two identical springs of spring constant $7580 \mathrm{N} {\mathrm{m}}^{-1}$ are attached to a block of mass $0.270 \mathrm{kg}$. What is the frequency of oscillation on the frictionless floor?

Hanging from a horizontal beam are nine simple pendulums of the following lengths : (a) $0.10 \mathrm{m}$, (b) $0.30 \mathrm{m}$, (c) $0.70 \mathrm{m}$, (d) $0.80 \mathrm{m}$, (e) $1.2 \mathrm{m}$, (f) $2.6 \mathrm{m}$, (g) $3.5 \mathrm{m}$, (h) $5.0 \mathrm{m}$ and (i) $6.2 \mathrm{m}$. Suppose the beam undergoes horizontal oscillations with angular frequencies in the range from $2.00 \mathrm{rad} {\mathrm{s}}^{-1}$ to $4.00 \mathrm{rad} {\mathrm{s}}^{-1}$. Which of the pendulums will be (strongly) set in motion?

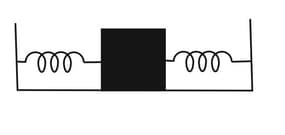
In the figure, two springs are attached to a block that can oscillate over a frictionless floor. If the left spring is removed, the block oscillates at a frequency of$30 \mathrm{Hz}$. If the spring on the right is removed, the block oscillates at a frequency of $50 \mathrm{Hz}$. At what frequency does the block oscillate with both springs attached?

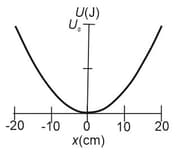
In the figure, gives the one-dimensional potential energy well for a $4.0 \mathrm{kg}$ particle (the function $U\left(x\right)$ has the form $b{x}^2$ and the vertical axis scale is set by $U_{\mathrm{s}}=2.0 \mathrm{J}$). $\left(a\right)$ If the particle passes through the equilibrium position with a velocity of $85 \mathrm{cm}/\mathrm{s}$, will it be turned back before it reaches $x=15 \mathrm{cm}$? $\left(b\right)$ If yes, at what position, and if no, what is the speed of the particle at $x=15 \mathrm{cm}$?

An oscillator consists of a block of mass $0.500 \mathrm{kg}$ connected to a spring. When set into oscillation with amplitude $35.0 \mathrm{cm}$, the oscillator repeats its motion every $0.350 \mathrm{s}$. Find the $\left(a\right)$ period, $\left(b\right)$ frequency, $\left(c\right)$ angular frequency, $\left(d\right)$ spring constant, $\left(e\right)$ maximum speed and $\left(f\right)$ magnitude of the maximum force on the block from the spring.

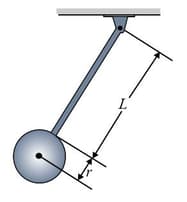
In the figure, a $5.00 \mathrm{kg}$ disk of diameter $\mathrm{D}=42.0 \mathrm{cm}$ is supported by a rod of length $\mathrm{L}=76.0 \mathrm{cm}$ and negligible mass that is pivoted at its end. (a) With the massless torsion spring unconnected, what is the period of oscillation? (b) With the torsion spring connected, the rod is vertical at equilibrium. What is the torsion constant of the spring if the period of oscillation has been decreased by $0.500 \mathrm{s}$?

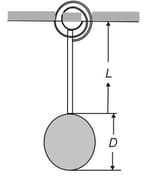
In the figure, the pendulum consists of a uniform disk with radius, $r=10.0 \mathrm{cm}$ and mass $500 \mathrm{g}$ attached to a uniform rod with length $L=500 \mathrm{mm}$ and mass $250 \mathrm{g}$.
(a) Calculate the rotational inertia of the pendulum about the pivot point. (b) What is the distance between the pivot point and the center of mass of the pendulum? (c) Calculate the period of oscillation.

A physical pendulum has a centre of oscillation at distance $2L/3$ from its point of suspension. Show that the distance between the point of suspension and the centre of oscillation for a physical pendulum of any form is $\frac{\mathit{I}}{\mathit{m}\mathit{h}}$, where $I$ is moment of inertia, $h$ is distance of centre of mass from the pivot point and $m$ is the mass of the pendulum.