Resnick & Halliday Solutions for Chapter: Waves-I, Exercise 1: Problems

A uniform rope of mass $m$ and length $L$ hangs from a ceiling.
(a) Show that the speed of a transverse wave on the rope is a function of $y$, the distance from the lower end, and is given by $v=\sqrt{gy}$
(b) Show that the time a transverse wave takes to travel the length of the rope is given by $t=2\sqrt{\frac{L}{g}}$

The speed of a transverse wave on a string is $115 \mathrm{m} {\mathrm{s}}^{-1}$ when the string tension is $200 \mathrm{N}$. To what value must the tension be changed to raise the wave speed to $223 \mathrm{m} {\mathrm{s}}^{-1}?$

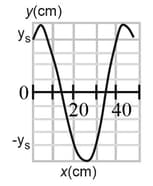
A sinusoidal transverse wave is traveling along a string in the negative direction of an $\mathrm{x}$ axis. In the Figure shown below shows a plot of the displacement as a function of position at time $\mathrm{t}=0$, the scale of the $\mathrm{y}$ axis is set by ${\mathrm{y}}_{\mathrm{s}}=4.0 \mathrm{cm}$. The string tension is $3.6 \mathrm{N}$, and its linear density is $28 \mathrm{g} {\mathrm{m}}^{-1}$. Find the
(a) amplitude.
(b) wavelength,
(c) wave speed, and (d) period of the wave.
(e) Find the maximum transverse speed of a particle in the string. 

If the wave is of the form $y(x, t)=y_{\mathrm{m}}\sin (kx\pm \omega t+\varphi ),$ what are

(f) $k$,

(g) $\omega$,
(h) $\mathrm{\varphi }$ and
(i) the correct choice of sign in front of $\mathrm{\omega }?$

Use the wave equation to find the speed of a wave given in terms of the general function $h(x, t)$
$y(x,t)=(4.00 \mathrm{mm})\sin \left[\left(22.0 {\mathrm{m}}^{-1}\right)x+\left(8.00 {\mathrm{s}}^{-1}\right)t\right]$.

A transverse sinusoidal wave is moving along a string in the positive direction of $x$ axis with a speed of $70 \mathrm{m} {\mathrm{s}}^{-1}$. At $t=0,$ the string particle at $x=0$ has a transverse displacement of $4.0 \mathrm{cm}$ and is not moving. The maximum transverse speed of the string particle at $x=0 \text{is} 16 \mathrm{m} {\mathrm{s}}^{-1}$.

(a) What is the frequency of the wave?
(b) What is the wavelength of the wave?

If $y(x,t)=y_{\mathrm{m}}\sin (kx\pm \omega t+\varphi )$ is the form of the wave equation, what are

(c)$y_{\mathrm{m}}$

(d)$k$

(e)${\omega }_0$

(f)$\varphi$

$\left(\mathrm{g}\right)$ the correct choice of sign in front of $\omega ?$

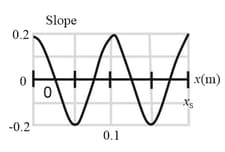
A sinusoidal wave travels along a string under tension. The figure shown below gives the slopes along the string at time $t=0.$ The scale of the $x$ axis is set by $x_{\mathrm{s}}=0.40 \mathrm{m}.$ What is the amplitude of the wave?

A string oscillates according to the equation,
$y^{\text{'}}=\left(0.80 \mathrm{cm}\right)\sin \left[\left(\frac{\mathrm{\pi }}{3} {\mathrm{cm}}^{-1}\right)x\right]\cos \left[\left(40\mathrm{\pi } {\mathrm{s}}^{-1}\right)t\right]$
What is the

$\left(\mathrm{a}\right)$ amplitude

$\left(\mathrm{b}\right)$ speed of the two waves (identical except the direction of travel) whose superposition gives this oscillation?

$\left(\mathrm{c}\right)$ What is the distance between nodes?

$\left(\mathrm{d}\right)$ What is the transverse speed of a particle of the string at the position $x=2.1 \mathrm{cm}$ when $t=0.50 \mathrm{s}$?

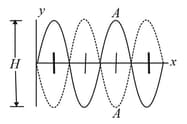
Two sinusoidal waves with the same amplitude and wavelength travel through each other along a string that is stretched along the $x$ axis. Their resultant wave is shown twice in the figure shown below, as the antinode $A$ travels from an extreme upward displacement to an extreme downward displacement in $6.0 \mathrm{ms}$. The tick marks along the axis are separated by $15 \mathrm{cm}$, height $H$ is $1.20 \mathrm{cm}.$ Let the equation for one of the two waves be of the form $y(x,t)=y_{\mathrm{m}}\sin (kx+\omega t).$ In the equation for the other wave, what are

(a) $y_m$

(b) $k$

(c) $\omega$

$\left(\mathrm{d}\right)$ the sign in front of $\mathrm{\omega }?$