I E Irodov Solutions for Chapter: ELECTRODYNAMICS, Exercise 4: ELECTRIC CURRENT

A long cylinder with uniformly charged surface and cross-sectional radius $a=1.0 \mathrm{cm}$, moves with a constant velocity $v=10 \mathrm{m} {\mathrm{s}}^{-1}$ along its axis. An electric field strength at the surface of the cylinder is equal to $E=0.9 \mathrm{kV} {\mathrm{cm}}^{-1}$. Find the resulting convection current, that is, the current caused by mechanical transfer of a charge.

An air cylindrical capacitor with a dc voltage $V=200 \mathrm{V}$ applied across it, is being submerged vertically into a vessel filled with water, at a velocity $v=5.0 \mathrm{mm} {\mathrm{s}}^{-1}$. The electrodes of the capacitor are separated by a distance $d=2.0 \mathrm{mm}$, the mean curvature radius of the electrodes is equal to $r=50\mathrm{mm}$. Find the current flowing in this case along the lead wires, if $d\ll r$. (Permittivity of vacuum, ${\epsilon }_0=0.885\times {10}^{-11} \mathrm{F} {\mathrm{m}}^{-1}$).

At temperature $0°\mathrm{C}$, the electric resistance of conductor $2$ is $\mathit{\text{η}}$ times that of conductor $1$. Their temperature coefficients of resistance are equal to ${\mathit{\text{α}}}_2$ and ${\mathit{\text{α}}}_1$, respectively. Find the temperature coefficient of resistance of a circuit segment consisting of these two conductors, when they are connected
(a) in series;
(b) in parallel.

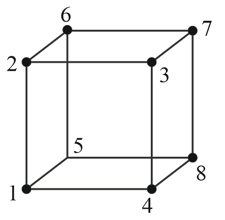
Find the resistance of a wire frame shaped as a cube (figure) when measured between points:
(a) $1-7$; (b) $1-2$; (c) $1-3$. The resistance of each edge of the frame is $R$.

At what value of the resistance $R_{\mathrm{x}}$, in the circuit shown in the figure, will the total resistance between points $A$ and $B$ be independent of the number of cells?

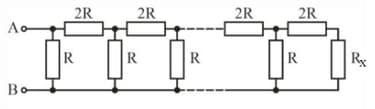
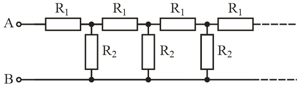
Figure shows an infinite circuit formed by the repetition of the same link, consisting of resistances $R_1=4.0 \mathrm{\Omega }$ and $R_2=3.0 \mathrm{\Omega }$. Find the resistance of this circuit between points $A$and $B$.

A copper wire carries a current of density, $j=1.0 \mathrm{A} {\mathrm{mm}}^{-2}$. Assuming that one free electron corresponds to each copper atom, evaluate the distance which will be covered by an electron during its displacement, $l=10 \mathrm{mm}$ along the wire ($e=1.6\times {10}^{-31} \mathrm{Kg}$).

A straight copper wire of length $l=1000 \mathrm{m}$ and cross-sectional area $S=1.0 {\mathrm{mm}}^2$ carries a current $I=4.5 \mathrm{A}$. Assuming that one free electron corresponds to each copper atom, find, 
$\left(a\right)$ the time it takes an electron to displace from one end of the wire to the other,
$\left(b\right)$ the sum of electric forces acting on all free electrons in the given wire.

( Take number of free electron per unit volume of copper $n=8.5\times {10}^{28} {\mathrm{m}}^{-3}$and resistivity of copper $\rho =1.77\times {10}^{-8} \mathrm{\Omega m}$, $e=1.6\times {10}^{-19} \mathrm{C}$ )