R K Bansal Solutions for Exercise 1: EXERCISE
R K Bansal Mathematics Solutions for Exercise - R K Bansal Solutions for Exercise 1: EXERCISE
Attempt the practice questions from Exercise 1: EXERCISE with hints and solutions to strengthen your understanding. Concise Mathematics I.C.S.E - Class IX solutions are prepared by Experienced Embibe Experts.
Questions from R K Bansal Solutions for Exercise 1: EXERCISE with Hints & Solutions
Given two equal chords and of a circle, with centre , intersecting each other at point . Prove that .
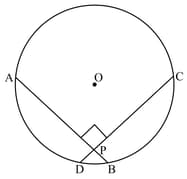
Given two equal chords and of a circle, with centre , intersecting each other at point . Prove that .
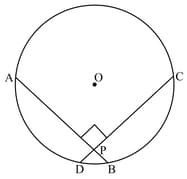
In a circle of radius and are two parallel chords of lengths and , respectively. If the distance between the chords (the chords are on the same side of the centre) is , find .
In a circle of radius and are two parallel chords of lengths and respectively. If the distance between the chords, if they are on the opposite sides of the centre is , find .
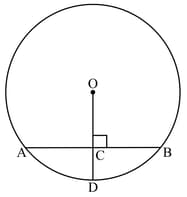
In the given figure, is the centre of the circle with radius and is perpendicular to . . If the length of is , find .
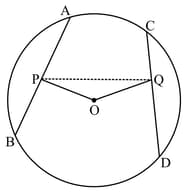
In the given figure, and are two equal chords of a circle, with centre . is the mid-point of chord is the mid-point of chord and . If , find .
In the given figure, is the diameter of the circle, with centre . Arc is half of arc . If , find .
The circumference of a circle, with centre , is divided into three arcs and such that . If , find .
