Resnick & Halliday Solutions for Chapter: Entropy and the Second Law of Thermodynamics, Exercise 1: Problems

 A two-stage Carnot engine consists of two Carnot cycles: In stage $1,$ a Carnot cycle absorbs heat at temperature $T_1=500 \mathrm{K}$  and discharges heat at temperature $T_2=400 \mathrm{K}$. In stage $2,$ a Carnot cycle absorbs that discharged heat at $T_2$ and then discharges heat at temperature $T_3=300 \mathrm{K}.$  What is the efficiency of the engine?

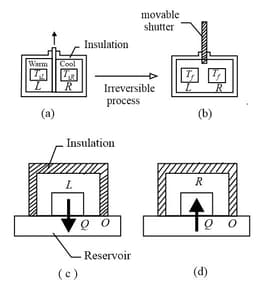
In the irreversible process of figures $a \& b$ let the initial temperatures of the identical blocks $L$ and $R$ be $305.5$ and $294.5\mathrm{K}$, respectively, and let $350$ $\mathrm{J}$ be the energy that must be transferred between the blocks in order to reach equilibrium. For the reversible processes of figures $c \& d$, what is $\Delta S$ (a) for block $L$, (b) its reservoir, (c) block $R,$ (d) its reservoir, (e) the two-block system, and (f) the system of the two blocks and the two reservoirs?

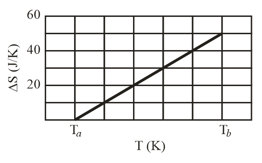
A $270 \mathrm{g}$ block is put in contact with a thermal reservoir. The block is initially at a lower temperature than the reservoir. Assume that the consequent transfer of energy as heat from the reservoir to the block is reversible. Figure (as shown below) gives the change in entropy $\mathrm{\Delta }S$ of the block, until thermal equilibrium is reached. The scale of the horizontal axis is set by $T_{\mathrm{a}}=280 \mathrm{K}$ and $T_{\mathrm{b}}=380 \mathrm{K}$. What is the specific heat of the block?

A Carnot engine operates between $235 °\mathrm{C}$ and $115 °\mathrm{C}$, absorbing $3.00\times {10}^4 \mathrm{J}$ per cycle, at the higher temperature.
(a) How much energy per cycle is discharged at the lower temperature? (b) How much work per cycle is this engine capable of performing?

A $6.0 \mathrm{g}$ ice cube at $-10 °\mathrm{C}$ is put into a thermos flask containing $100 {\mathrm{cm}}^3$ of water at $20 °\mathrm{C}$. By how much has the entropy of the cube-water system changed when equilibrium is reached? The specific heat of ice is $2220 \mathrm{J} {\mathrm{kg}}^{-1} {\mathrm{K}}^{-1}$.

Suppose $2.00 \mathrm{mol}$ of an ideal gas undergoes a reversible isothermal compression from volume $V_1$ to volume $V_2=0.500 V_1$, at temperature $T=400 \mathrm{K}$.  Find

$\left(\mathrm{a}\right)$ the work done by the gas and
$\left(\mathrm{b}\right)$ the entropy change of the gas. $\left(\mathrm{c}\right)$ If the compression is reversible and adiabatic instead of isothermal, what is the entropy change of the gas?

(a) What is the entropy change of a $15.0 \mathrm{g}$ ice cube that melts completely in a bucket of water, whose temperature is just above the freezing point of water? (b) What is the entropy change of a $5.00 \mathrm{g}$ spoonful of water that evaporates completely on a hot plate whose temperature is slightly above the boiling point of water? (Use:For ice $L=333 \mathrm{J} {\mathrm{g}}^{-1}$ and for vapour $L=2256 \mathrm{J} {\mathrm{g}}^{-1}$)

A $20 \mathrm{g}$ ice cube at $-15 °\mathrm{C}$ is placed in a lake whose temperature is $15 °\mathrm{C}$. Calculate the change in the entropy of the cube-lake system as the ice cube comes to thermal equilibrium with the lake. The specific heat of ice is $2220 \mathrm{J} {\mathrm{kg}}^{-1} {\mathrm{K}}^{-1}$. (Hint: Will the ice cube affect the lake temperature?)