Resnick & Halliday Solutions for Chapter: Induction and Inductance, Exercise 1: Problems

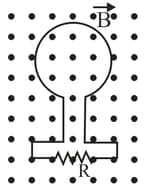
A solenoid having an inductance of $9.70 \mu \mathrm{H}$ is connected in series with a $1.20 \mathrm{k\Omega }$ resistor.

$\text{(a)}$ If a $14.0 \mathrm{V}$ battery is connected across the pair, how long will it take for the current through the resistor to reach $40.0\%$ of its final value?
$\left(b\right)$ What is the current through the resistor at time $t=0.50 {\tau }_L$? 

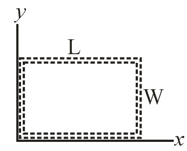
In the given figure, a wire loop of lengths $L=50.0 \mathrm{cm}$ and $W=20.0 \mathrm{cm}$ lies in a magnetic field $\overrightarrow{B}$. What are the
$\left(\mathrm{a}\right)$ Magnitude of induced EMF $\epsilon$ and $\left(b\right)$ direction (clockwise or counterclockwise or none if $\epsilon =0$) of the emf induced in the loop, if $\overrightarrow{B}=\left(4.00\times {10}^{-2} \mathrm{T} {\mathrm{m}}^{-1 }\right)y \hat{\mathrm{k}}$ ? What are $\left(\mathrm{c}\right)$ $\epsilon$ and $\left(\mathrm{d}\right)$ the direction, if $\overrightarrow{B}=\left(6.00\times {10}^{-2} \mathrm{T} {\mathrm{s}}^{-1}\right)t \hat{\mathrm{k}}?$ What are $\left(e\right)$$\epsilon$ and $\left(f\right)$  the direction, if $\overrightarrow{B}=\left(8.00\times {10}^{-2} \mathrm{T} {\mathrm{m}}^{-1} {\mathrm{s}}^{-1}\right)yt \hat{\mathrm{k}}$ ? What are $\left(g\right) \epsilon$ and $\left(\mathrm{h}\right)$ the direction, if $\overrightarrow{B}=\left(3.00\times {10}^{-2}\mathrm{T} {\mathrm{m}}^{-1} {\mathrm{s}}^{-1}\right)xt \hat{\mathrm{j}}$? What are $\left(i\right)$ $\epsilon$ and $\left(j\right)$ the direction, if $\overrightarrow{B}=\left(5.00\times {10}^{-2} \mathrm{T} {\mathrm{m}}^{-1} {\mathrm{s}}^{-1})\right.$$yt \hat{\mathrm{i}}$?  

A solenoid that is $85.0 \mathrm{cm}$ long has a cross-sectional area of $17.0 {\mathrm{cm}}^2$. There are $1210$ turns of wire carrying a current of  $6.60 \mathrm{A}$ $\left(\mathrm{a}\right)$ Calculate the energy density of the magnetic field inside the solenoid. $\left(\mathrm{b}\right)$ Find the total energy stored in the magnetic field there (neglect end effects).

Figure (a) shows a circuit consisting of an ideal battery with emf $\epsilon =6.00 \mathrm{\mu V}$, a resistance $R,$ and a small wire loop of area $5.0 {\mathrm{cm}}^2$. For the time interval $t=10 \mathrm{s}$ to $t=20 \mathrm{s}$, an external magnetic field is set up throughout the loop. The field is uniform, its direction is into the page in Figure (a) and the field magnitude is given by $B=at$, where $B$ is in $\mathrm{tesla}$, $a$ is a constant and $t$ is in seconds. Figure (b) gives the current $i$ in the circuit before, during and after the external field is set up. The vertical axis scale is set by $i_{\mathrm{s}}=4.0 \mathrm{mA}$. Find the constant $a$ in the equation for the field magnitude. 

$\left(\mathrm{a}\right)$  $\left(\mathrm{b}\right)$ 

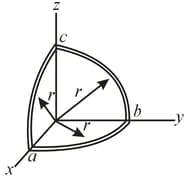
A wire is bent into three circular segments, each of radius $r=10 \mathrm{cm},$ as shown in figure. Each segment is a quadrant of a circle, $ab$ lying in the $xy$ plane, $bc$ lying in the $yz$ plane, and $ca$ lying in the $zx$-plane. (a) If a uniform magnetic field $\overrightarrow{B}$ points in the positive $x$-direction, what is the magnitude of the emf developed in the wire when $B$ increases at the rate of $9.0 \mathrm{mT} {\mathrm{s}}^{-1}$?
(b) What is the direction of the current in segment $bc$?

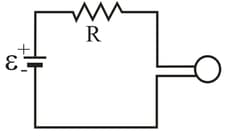
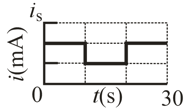
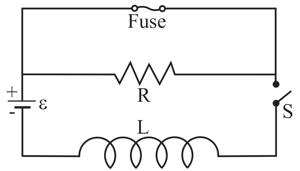
In Fig. $R=15 \Omega \text{,} L=15 \mathrm{H}$ the ideal battery has, $\epsilon =10 \mathrm{V}$, and the fuse in the upper branch is an ideal $3.0 \mathrm{A}$ fuse. It has zero resistance as long as the current through it remains less than $3.0 \mathrm{A}$. If the current reaches $3.0 \mathrm{A}$, the fuse "blows" and thereafter has infinite resistance. Switch $S$ is closed at time $t=0$.
(a) When does the fuse blow? (b) Sketch a graph of the current $i$ through the inductor as a function of time. Mark the time at which the fuse blows.

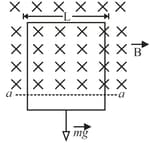
In the given figure, a long rectangular conducting loop, of width $L$ resistance $R$ and mass $m,$ is hung in a horizontal, uniform magnetic field $\overrightarrow{B}$ that is directed into the page and that exists only above line $aa$. The loop is then, dropped during its fall, it accelerates until it reaches a certain terminal speed $v_t$. Ignoring air drag, find an expression for $v_t$.

In the given figure, the magnetic flux through the loop increases according to the relation ${\varphi }_{\mathrm{B}}=3.0t^2+7.0t$ where ${\varphi }_{\mathrm{B}}$ is in $\mathrm{mWb}$ and $t$ is in $\mathrm{s}$.
$\left(\mathrm{a}\right)$ What is the magnitude of the emf induced in the loop when $t=1.5 \mathrm{s}$?
$\left(\mathrm{b}\right)$ Is the direction of the current through $R$ to the right or left?