S S Krotov Solutions for Chapter: Heat and Molecular Physics, Exercise 1: Exercise

The shell of a space station is a blackened sphere in which a temperature $T=500 \mathrm{K}$ is maintained due to the operation of appliances of the station. The amount of heat given away from a unit surface area is proportional to the fourth power of thermodynamic temperature.

Determine the temperature $T_x$ of the shell if the station is enveloped by a thin spherical black screen of nearly the same radius as the radius of the shell.

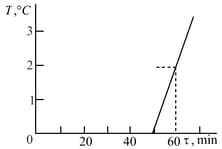
A bucket contains a mixture of water and ice of mass $m=10 \mathrm{kg}$ The bucket is brought into a room, after which the temperature of the mixture is immediately measured. The obtained $T\left(\tau \right)$ dependence is plotted in Fig. The specific heat of water is $c_{\mathrm{w}}=4.2 \mathrm{J} {\left(\mathrm{kg}·\mathrm{K}\right)}^{-1}$, and the latent heat of fusion of ice is $\lambda =340 \mathrm{kJ} {\mathrm{kg}}^{-1}$. Determine the mass $m_{\mathrm{ice}}$ of ice in the bucket at the moment it is brought in the room, neglecting the heat capacity of the bucket.

The properties of a nonlinear resistor were investigated in a series of experiments. At first, the temperature dependence of the resistor was studied. As the temperature was raised to $T_1=100 °\mathrm{C}$, the resistance changed jump wise from $R_1=50 \mathrm{\Omega }$ to $R_2=100 \mathrm{\Omega }$. The reverse abrupt change upon cooling took place at $T_2=99 °\mathrm{C}$. Then a d.c. voltage $U_1={60}^2 \mathrm{V}$ was applied to the resistor. Its temperature was found to be $T_3=80 °\mathrm{C}$. Finally, when a d.c. voltage $U_2=80 \mathrm{V}$ was applied to the resistor, spontaneous current oscillations were observed in the circuit. The air temperature $T_0$ in the laboratory was constant and equal to $20 °\mathrm{C}$. The heat transfer from the resistor was proportional to the temperature difference between the resistor and the ambient, the heat capacity of the resistor being $C=3 \mathrm{J} {\mathrm{K}}^{-1}$. Determine the period $T$ of current oscillations and the maximum and minimum values of the current.

When raindrops fall on a red-brick wall after dry and hot weather, hissing sounds are produced.

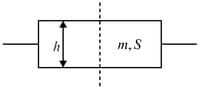
A thin-walled cylinder of mass $m$, height $h$, and cross-sectional area $S$ is filled with a gas and floats on the surface of the water. As a result of leakage from the lower part of the cylinder, the depth of its submergence has increased by, $\Delta h$. Determine the initial pressure, $p_1$ of the gas in the cylinder if the atmospheric pressure is $p_0$, and the temperature remains unchanged.

A shock wave is the region of an elevated pressure propagating in the positive direction of the $x$-axis at a high velocity $v$.

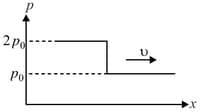
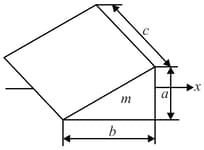
At the moment of arrival of the wave, the pressure abruptly increases. This dependence is plotted in the figure. Determine the velocity $u$ acquired by a wedge immediately after the shock front passes through it. The mass of the wedge is $m$, and its size is shown in the figure. Friction should be neglected, and the velocity acquired by the wedge should be assumed to be much lower than the velocity of the wave $\left(u\ll v\right)$.

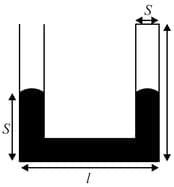
A thin U-tube sealed at one end consists of three bends of length, $l=250 \mathrm{mm}$ each, forming right angles. The vertical parts of the tube are filled with mercury to half the height (Fig). All mercury can be displaced from the tube by heating slowly the gas in the sealed end of the tube, which is separated from the atmospheric air by mercury. Determine the work $A$ done by the gas thereby if the atmospheric pressure is, $p_0={10}^5 \mathrm{Pa}$ , the density of mercury is, ${\rho }_{\mathrm{mer}}=13.6\times {10}^3 \mathrm{kg} {\mathrm{m}}^{-3}$, and the cross-sectional area of the tube is, $S=1{ \mathrm{cm}}^2$.

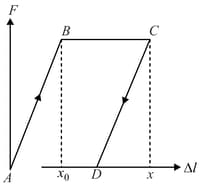
The residual deformation of an elastic rod can be roughly described by using the following model. If the elongation of the rod $\Delta l<x_0$ (where $x_0$ is the quantity present for the given rod), the force required to cause the elongation $\Delta l$ is determined by Hooke's law: $F=k\Delta l$, where $k$ is the rigidity of the rod. If $\Delta l>x_0$, the force does not depend on elongation any longer (the material of the rod starts "flowing"). If the load is then removed, the elongation of the rod will decrease along $CD$ which for the sake of simplicity will be taken straight and parallel to the segment $AB$ (Fig). Therefore, after the load has been removed completely, the rod remains deformed (point $D$ in the figure). Let us suppose that the rod is initially stretched by $\Delta l=x>x_0$ and then the load is removed. Determine the maximum change $\Delta T$ in the rod temperature if its heat capacity is $C$, and the rod is thermally insulated.