CAT - Test Questions Helping You Bell the CAT

Let there be a circle with centre $\mathrm{O}$ and radius $\mathrm{r},$ such that the four points. $\mathrm{A}, \mathrm{B}, \mathrm{C}$ and $\mathrm{D}$ are cyclic while $\mathrm{AC}$ and $\mathrm{BD}$ are the two chords intersecting each other perpendicularly at a point $\mathrm{P}$ somewhere inside the circle. If $\mathrm{A}, \mathrm{B}, \mathrm{C}$ and $\mathrm{D}$ are variable points and $\mathrm{OP}=\mathrm{d},$ find the maximum and minimum area of the quadrilateral $\mathrm{ABCD}.$

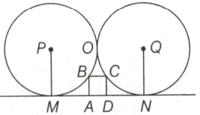
There are two circles ${\mathrm{C}}_1$ and ${\mathrm{C}}_2$ of radii ${\mathrm{r}}_1$ and ${\mathrm{r}}_2,$ respectively. They are mutually tangent to each other and to a line as well. There is one more circle of radius ${\mathrm{r}}_3$ which is tangent to this line and the first two circles ${\mathrm{C}}_1$ and $C_2.$ What is the relation between the three radii ${\mathrm{r}}_1, {\mathrm{r}}_2$ and ${\mathrm{r}}_3 ?$

Two equal circles with centers $\mathrm{P}$ and $\mathrm{Q}$ are tangent at $\mathrm{O} . \mathrm{A}$ common line is tangent to both the circles at $\mathrm{M}$ and $\mathrm{N}$ respectively. Point $\mathrm{B}$ lies on the arc $\mathrm{OM}$ and point $\mathrm{C}$ lies on the arc $\mathrm{ON}.$ Points $\mathrm{A}$ and $\mathrm{D}$ lie on the tangent $\mathrm{MN}.$ If the radius of each circle is $\mathrm{r}$ and each side of the square $\mathrm{ABCD}$ is $\mathrm{x},$ find $\mathrm{x}.$

In the following diagram four circles are tangent to every other circle. The radius of each of the circles $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$ is $1.$ Find the radius of circle $\mathrm{D},$ which is tangent to all the three given circles and lies at the centre.

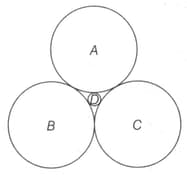
In the following diagram there are three circles packed in another circle, such that each circle is tangent to all other circles in this arrangement. The radius of the circumscribing circle $\mathrm{A}$ is $1 \mathrm{cm};$ and circle $\mathrm{B}$ and circle $\mathrm{C}$ are congruent. Find the radius of the circle $\mathrm{D}.$

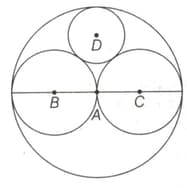
In the following diagram there are four circles $\mathrm{A}, \mathrm{B}, \mathrm{C}$ and $\mathrm{D}$ packed in a circle $\mathrm{P}.$ The radius of the circumscrib $\mathrm{g}$ circle $\mathrm{P}$ is $1 \mathrm{cm}.$ Circles $\mathrm{A}$ anc $\mathrm{B}$ are tangent at $\mathrm{P},$ the centre of the circumscribing circle. Circle $\mathrm{D}$ is tangent to circles $\mathrm{A}, \mathrm{C}$ and $\mathrm{P}.$ Find the radius of the circle $\mathrm{D}.$

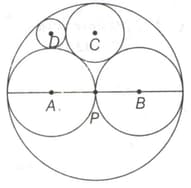
There are three circles, with radii $1 \mathrm{cm}, 2 \mathrm{cm}$and $3 \mathrm{cm},$ tangent to each other. Find the radius of the fourth circle, which is tangent to all the existing circles.

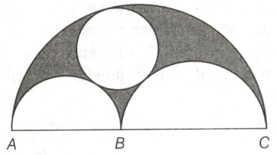
In the following diagram, a semicircle of radius $\mathrm{r}$ inscribes two semicircles, which are tangent to each other at a point $\mathrm{B}$ on the diameter $\mathrm{AC}$ of the larger semicircle. Then there is a full circle inscribed in the remaining area, which is tangent to all the three existing semicircles. Find the radius of this full circle, if the diameter $\mathrm{AB}=\frac{1}{3} \mathrm{cm}$ and $\mathrm{BC}=\frac{2}{3} \mathrm{cm}$