Sue Pemberton Solutions for Chapter: Further Differentiation, Exercise 9: END-OF-CHAPTER REVIEW EXERCISE 8
Sue Pemberton Mathematics Solutions for Exercise - Sue Pemberton Solutions for Chapter: Further Differentiation, Exercise 9: END-OF-CHAPTER REVIEW EXERCISE 8
Attempt the practice questions on Chapter 8: Further Differentiation, Exercise 9: END-OF-CHAPTER REVIEW EXERCISE 8 with hints and solutions to strengthen your understanding. Cambridge International AS & A Level Mathematics : Pure Mathematics 1 Course Book solutions are prepared by Experienced Embibe Experts.
Questions from Sue Pemberton Solutions for Chapter: Further Differentiation, Exercise 9: END-OF-CHAPTER REVIEW EXERCISE 8 with Hints & Solutions
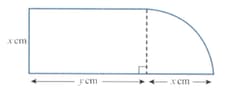
The diagram shows a metal plate consisting of a rectangle with sides cm and cm and a quarter-circle of radius cm. The perimeter of the plate is cm.Given that can vary, find this stationary value of and determine whether it is a maximum or a minimum value.
A curve has equation: . Find the set of values of for which the gradient of the curve is less than .
A curve has equation: . Find the coordinates of the two stationary points on the curve and determine the nature of each stationary point.
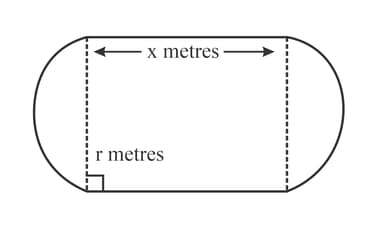
The inside lane of a school running track consists of two straight sections each of length metres, and two semicircular sections each of radius metres, as shown in the diagram. The straight sections are perpendicular to the diameters of the semicircular sections. The perimeter of the inside lane is metres. Show that the area,, of the region enclosed by the inside lane is given by .
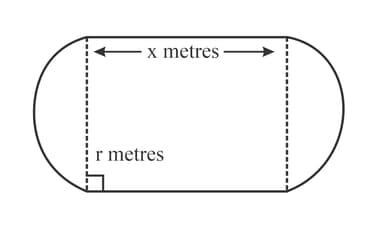
The inside lane of a school running track consists of two straight sections each of length metres, and two semicircular sections each of radius metres, as shown in the diagram. The straight sections are perpendicular to the diameters of the semicircular sections. The perimeter of the inside lane is metres. Given that and can vary, show that, when has a stationary value, there are no straight sections in the track. Determine whether the stationary value is a maximum or a minimum.
The equation of a curve is , where is a positive constant. Show that the origin is a stationary point on the curve and find the coordinates of the other stationary point in terms of .
The equation of a curve is , where is a positive constant. Find the stationary points on the curve and determine nature of each of the stationary points.
The curve has equation . Find the set of values of for which this curve has no stationary points.
