Sue Pemberton, Julianne Hughes and, Julian Gilbey Solutions for Chapter: Logarithmic and Exponential Functions, Exercise 10: END-OF-CHAPTER REVIEW EXERCISE 2
Sue Pemberton Mathematics Solutions for Exercise - Sue Pemberton, Julianne Hughes and, Julian Gilbey Solutions for Chapter: Logarithmic and Exponential Functions, Exercise 10: END-OF-CHAPTER REVIEW EXERCISE 2
Attempt the free practice questions on Chapter 2: Logarithmic and Exponential Functions, Exercise 10: END-OF-CHAPTER REVIEW EXERCISE 2 with hints and solutions to strengthen your understanding. Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book solutions are prepared by Experienced Embibe Experts.
Questions from Sue Pemberton, Julianne Hughes and, Julian Gilbey Solutions for Chapter: Logarithmic and Exponential Functions, Exercise 10: END-OF-CHAPTER REVIEW EXERCISE 2 with Hints & Solutions
The polynomial is defined by .
Show that and factorise completely.
The polynomial is defined by .
Given that , state the value of and hence find correct to significant figures.
Solve the equation , giving your answer correct to significant figures.
Use logarithms to solve the equation , giving your answer correct to decimal places.
Using the substitution , solve the equation giving your answer correct to significant figures.
The variables and , satisfy the equation .
By taking natural logarithms, show that the graph of against , is a straight line and find the exact value of the gradient of this line.
The variables and satisfy the equation .
This line intersects the -axis at and the -axis at . Find the exact coordinates of the midpoint of .
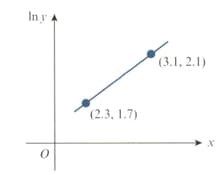
The variables and satisfies the equation , where and are constants. The graph of against is a straight line passing through the points and , as shown in the diagram. Find the values of and , correct to decimal places.
