Sue Pemberton, Julianne Hughes and, Julian Gilbey Solutions for Chapter: Numerical Solutions of Equations, Exercise 5: END-OF-CHAPTER REVIEW EXERCISE 6

Write down an iterative formula based on the equation $x=\sqrt[5]{\frac{8}{x}-x}$. Use this formula, with a starting value $\beta =-1.5$ to find the value of $\beta$ correct to $3$ significant figures. Give the result of each iteration to $5$ significant figures.

Show that the equation sec $x=\left(\frac{\pi }{2}-x\right)\left(\frac{\pi }{4}+x\right)$ can be written in the form $x=\sqrt{\frac{2\pi x+{\pi }^2-8\sec x}{8}}.$

The two real roots of the equation $\sec x=\left(\frac{\pi }{2}-x\right)\left(\frac{\pi }{4}+x\right)$ in the interval $-\frac{\pi }{2}<x⩽\frac{\pi }{2}$ are denoted $\alpha$ and $\beta .$ Verify by calculation that the smaller root, $\alpha ,$ is $-0.21$ correct to $2$ decimal places.

The two real roots of the equation $\sec x=\left(\frac{\pi }{2}-x\right)\left(\frac{\pi }{4}+x\right)$ in the interval $-\frac{\pi }{2}<x⩽\frac{\pi }{2}$ are denoted $\alpha$ and $\beta .$ Using an iterative formula based on the equation given with an initial value of $1,$ find the value of $\beta$ correct to $2$ decimal places. Give the result of each iteration to $4$ decimal places.

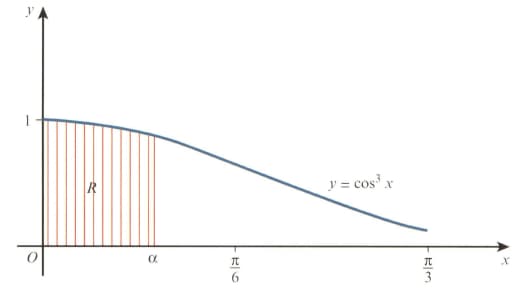
The diagram shows part of the curve $y={\cos }^{3}x,$ where $x$ is in radians. The shaded region between the curve, the axes and the line $x=\alpha$ is denoted by $R.$ The area of $R$ is equal to $0.3.$

Using the substitution $u=\sin x,$ find ${\int }_0^{\alpha }{\cos }^{3}x \mathrm{d}x.$ Hence show that $\sin \alpha =\frac{0.9}{3-{\sin }^2\alpha }.$

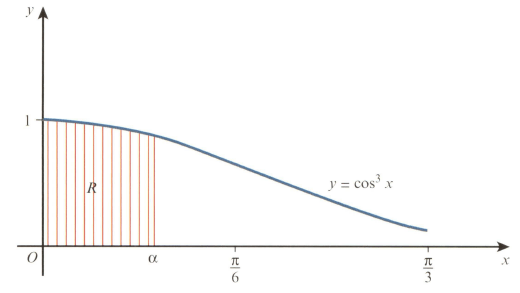
The diagram shows part of the curve $y={\cos }^{3}x,$ where $x$ is in radians. The shaded region between the curve, the axes and the line $x=\alpha$ is denoted by $R.$ The area of $R$ is equal to $0.3.$

Use the iterative formula ${\alpha }_{n+1}={\sin }^{-1}\left(\frac{0.9}{3-{\sin }^2{\alpha }_n}\right)$ with ${\alpha }_1=0.2,$ to find the value of $\alpha$ correct to $3$ significant figures. Give the result of each iteration to $5$ significant figures.

It is given that ${\int }_1^a\ln x \mathrm{d}x=5,$ where $a$ is a constant greater than $1 .$

Show that $a=\frac{4+a}{\ln a}.$

It is given that ${\int }_1^a\ln x \mathrm{d}x=5,$ where $a$ is a constant greater than $1 .$

Use an iterative formula based on the equation in to find the value of $a$ correct to $3$ decimal places. Use an initial value of $5$ and give the result of each iteration to $5$ decimal places.

Data: $\ln \left(5\right)=1.6094$, $\ln (5.59201)\approx 1.73906, \ln (5.57241)\approx 1.71782 \mathrm{and} \ln (5.57239)\approx 1.71782$