Sue Pemberton, Julianne Hughes and, Julian Gilbey Solutions for Chapter: Trigonometry, Exercise 4: EXERCISE 3C
Author:Sue Pemberton, Julianne Hughes & Julian Gilbey
Sue Pemberton Mathematics Solutions for Exercise - Sue Pemberton, Julianne Hughes and, Julian Gilbey Solutions for Chapter: Trigonometry, Exercise 4: EXERCISE 3C
Attempt the free practice questions on Chapter 3: Trigonometry, Exercise 4: EXERCISE 3C with hints and solutions to strengthen your understanding. Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book solutions are prepared by Experienced Embibe Experts.
Questions from Sue Pemberton, Julianne Hughes and, Julian Gilbey Solutions for Chapter: Trigonometry, Exercise 4: EXERCISE 3C with Hints & Solutions
EASY
AS and A Level
IMPORTANT
Express and in terms of Hence show that is a root of the equation
EASY
AS and A Level
IMPORTANT
Find the exact value of Given that is a root of the equation
EASY
AS and A Level
IMPORTANT
Find the range of values of between and for which
EASY
AS and A Level
IMPORTANT
Solve the inequality for
EASY
AS and A Level
IMPORTANT
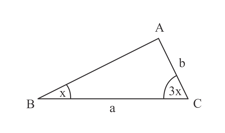
Prove that
EASY
AS and A Level
IMPORTANT
Use the expansions of and to prove that:
EASY
AS and A Level
IMPORTANT
Use the expansions of and to prove that:
Solve for
EASY
AS and A Level
IMPORTANT
Solve the inequality for
