West Bengal Board Solutions for Chapter: Concept of Vertically Opposite Angles, Exercise 1: Let's work out - 7.1

Write the measurement of $\angle BOD, \angle BOC$ and $\angle AOC$.

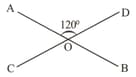
Sum of the measurement of $\angle POR$ and $\angle QOS$ is $110°$. Let's write the measurement of $\angle POS, \angle QOS, \angle QOR$ and $\angle POR$.

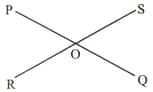
$OP, OQ, OR$ and $OS$ are concurrent. $OP$ and $OR$ are on a same straight line. $P$ and $R$ are situated on opposite sides of the point $O$. $\angle POQ=\angle ROS$ and $\angle POQ\ne \angle QOR$. If $\angle POQ=50°$ then write the measurement of $\angle QOR, \angle ROS$ and $\angle POS$.

Four rays meet at a point in such a way that measurement of opposite angles are equal. Let's prove that two straight lines are formed by those four rays.

Let's prove that internal and external bisectors of an angle are perpendicular to each other.

If two straight lines intersect each other than four angles are formed. Let's prove that the sum of measurement of the four angles is four right angles.

In triangle$△PQR$, $\angle PQR=\angle PRQ$, if we extend $QR$ on both sides then two exterior angles are formed. Let's prove that the measurement of external angles are equal.

Two straight lines intersect each other at a point and thus four angles are formed. Let's prove that the bisectors of these angles are two perpendicular straight lines.