West Bengal Board Solutions for Chapter: Relation Between Two Sides of a Triangle and Their Opposite Angles, Exercise 1: let's workout - 9

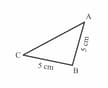
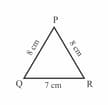
Let's see the isosceles triangle given below and without measuring let's write which two sides are equal in length in each triangle.

Let's see the isosceles triangle given below and without measuring let's write which two angles are equal in measurement in each triangle.
     

Line segments $AB$ and $CD$ bisect each other at $O$. Let's prove that $AC$ and $BD$ are parallel. Let's write what kind of quadrilateral is $ABCD$.

E and F are two points of two parallel straight lines AB and CD respectively. O is the midpoint of line segment EF. We draw a straight line passing through O which intersect AB and CD at P and Q respectively. Let's prove that O bisects the line segment PQ.

If we produce the base of an isosceles triangle on both sides then two exterior angles are formed. Let's prove that they are equal in measurement.

Let's prove that the medians of the equilateral triangle are equal.

In a trapezium ABCD, AD||BC and angle ABC= angle BCD. Let's prove that ABCD is an isosceles trapezium.

Two line segments $PQ$ and $RS$ intersect each other at $X$ in such a way that $XP=XR$ and $\angle PSX=\angle RQX$. Let's prove that $△PXS\cong △RQX$.