EASY
Earn 100
"The maximum or the minimum of the objective function occurs only at the corner points of the feasible region". This theorem is known as fundamental theorem of
(a)Algebra
(b)Arithmetic
(c)Calculus
(d)Extreme points
70% studentsanswered this correctly
Important Questions on Linear Programming
MEDIUM
HARD
EASY
EASY
EASY
EASY
MEDIUM
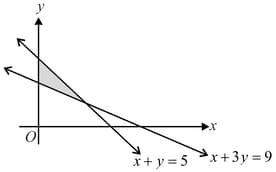
MEDIUM
The shaded region is the solution set of the inequalities
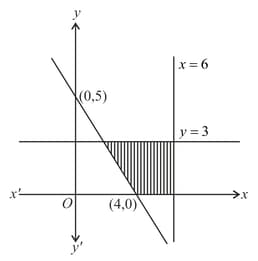
HARD
EASY
EASY
HARD
The maximum value of subject to is
HARD
EASY
The feasible region of an is shown in the figure. If , then the minimum value of occurs at
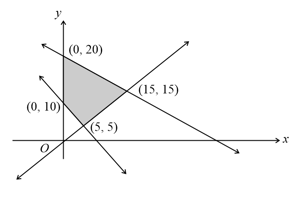
MEDIUM
Minimize Subject to : and
Which one of the following points lies outside the feasible region?
EASY
Solve graphically the following linear programming problem:
Maximize or minimize subject to constraints .
HARD
A furniture trader deals in only two items - chairs and tables. He has rupees to invest and a space to store at most items. A chair costs him rupees and a table costs him rupees . The trader earns a profit of rupees and rupees on a chair and table, respectively. Formulate the above problem as an LPP to maximise the profit and solve it graphically.
MEDIUM
EASY
HARD

