Discuss about pile of plates.
 

1. Newton's Corpuscular Theory:

(i) Light is made up of tiny, light, and elastic particles called corpuscles which are emitted by a luminous body.

(ii) The corpuscles travels with speed of light in all directions in straight lines.

(iii) The corpuscles carry energy and when hits retina of the eye, they produce sensation of vision.

(iv) Corpuscles are of different colours & different sizes (red corpuscles larger than blue corpuscles).

(v) The theory explains,

(a) that light carry energy and momentum

(b) that light travels in a straight line

(c) propagation of light in vacuum

(d) laws of reflection and refraction

(vi) The theory fails to explain interference, diffraction, and polarization.

(vii) A major prediction of the corpuscular theory is that the speed of light in a denser medium is more than the speed of light in a rarer medium which is wrong.

2. Huygen's Wave Theory:

(i) Huygen's in 1678 assumed that light propagates in the form of wavefronts.

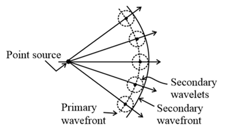
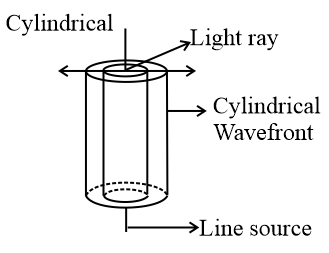
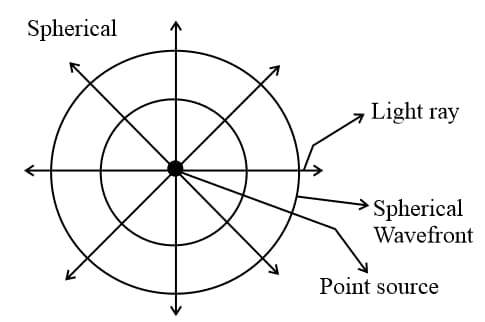
(ii) Each point source of light is a centre of disturbance from which waves spread in all directions. The locus of all the particles of the medium vibrating in the same phase at a given instant is called a wavefront.

(iii) Each point on a wavefront is a source of new disturbance, called secondary wavelets. These wavelets are spherical and travel with the speed of light in that medium.

(iv) The forward envelope of the secondary wavelets at any instant gives the new wavefront.

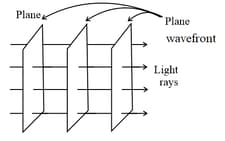
(v) In a homogeneous medium, the wavefront is always perpendicular to the direction of wave propagation.

3. Wavefront:

(i) The locus of all particles in a medium, vibrating in the same phase is called wavefront.

(ii) The direction of propagation of light is perpendicular to the wavefront.

(iii) Every point on the given wavefront acts as a source of a new disturbance called secondary wavelets which travel in all directions with the velocity of light in the medium.

(iv) A surface touching these secondary wavelets tangentially in the forward direction at any instant gives the new wavefront at that instant, called secondary wavefront.

4. Reflection and Refraction of Wavefront:

(i) Reflection:

Length $\mathrm{BC}=\mathrm{AE}$ and ∠ i=∠ r

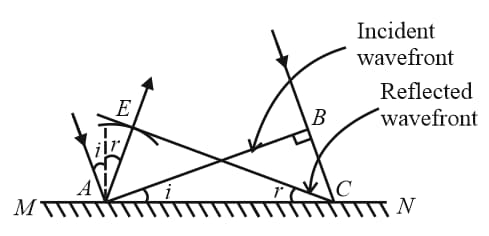
(ii) Refraction:

Ratio of length $\frac{\mathrm{BC}}{\mathrm{AE}}=\frac{v_1}{v_2}=\frac{\sin i}{\sin r}$

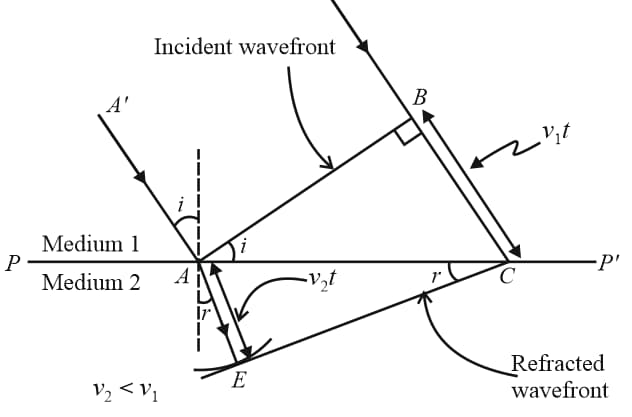
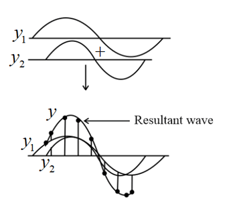
5. Superposition of Waves:

When two or more than two waves superimpose over each other then the resultant displacement $\left(y\right)$ is equal to the vector sum of the displacements (y→1 and y→2) produced by individual waves at that point, i.e., $\overrightarrow{y}={\overrightarrow{y}}_1+{\overrightarrow{y}}_2$

6. General Terms:

(i) Phase: For displacement expression, $y=a\sin \left(\omega t\right)$, where ωt= phase or instantaneous phase of the wave, $\omega =$angular frequency of the wave, $a=$amplitude of the wave, $t=$time

(ii) Phase difference ϕ: The difference between the phases of two waves, i.e., if $y_1=a_1\sin \omega t$ and $y_2=a_2\sin \left(\omega t+\varphi \right)$, so phase difference=ϕ, where $a_1=$amplitude of the first wave, $a_2=$amplitude of the second wave

(iii) Relation between phase difference $\left(\varphi \right)$ & path difference $\left(∆x\right)$: $\frac{∆x}{\lambda }=\frac{\varphi }{2\mathrm{\pi }}$, where $\lambda =$wavelength of the light used

(iv) Coherent source of light: Two sources are said to be coherent when the waves emitted from them have the same frequency and constant phase difference.

7. Interference of Light:

When two waves of the same frequency (coming from two coherent sources) travel in a medium, in the same direction simultaneously then due to their superposition, at some points intensity of light is maximum while at some other points intensity is minimum. This phenomenon is called Interference of light.

(i) Constructive interference (maximum intensity case):

(a) Phase difference, $\varphi =0°$ or $2n\mathrm{\pi }$, where $n=1, 2, 3 ...$

(b) Path difference, $\mathrm{\Delta }x=n\lambda$, i.e., even multiple of $\lambda /2$ and $n=1, 2, 3,...$

(c) Resultant amplitude, $A_{\max }=a_1+a_2$. If $a_1=a_2=a_0$ then $A_{\max }=2a_0$, where $a_1=$amplitude of the first wave, $a_2=$amplitude of the second wave

(d) Resultant intensity, $I_{\mathrm{net}}=I_1+I_2+2\sqrt{I_1{I}_2}\cos \left(\varphi \right)$, where $I_1=$intensity of the first wave, $I_2=$intensity of the second wave

Therefore, $I_{\max }=I_1+I_2+2\sqrt{I_1{I}_2}=\left(\sqrt{I_1}+\sqrt{I_2}\right){ }^2$

If $I_1=I_2=I_0$ then $I_{\max }=4I_0$

(ii) Destructive interference (minimum intensity case):

(a) Phase difference $\varphi =180°$or $\left(2n-1\right)\mathrm{\pi }$, where $n = 1, 2, 3,...$ or $\left(2n+1\right)\mathrm{\pi }$

(b) Path difference Δ=2n-1λ2, i.e., odd multiple of λ/2

(c) Resultant amplitude, $A_{\min }=a{ }_1-a{ }_2$. If $a{ }_1=a{ }_2\Rightarrow A_{\min }=0$

(d) Resultant intensity, $I_{\min }=I_1+I_2-2\sqrt{I_1{I}_2}=\left(\sqrt{I_1}-\sqrt{I_2}\right){ }^2$. If $I_1=I_2=I_0\Rightarrow I_{\min }=0$

(iii) No interference pattern is produced with the superposition of waves of random phase difference. Resultant intensity is just the sum of the two intensities, $I=I_1+I_2$

8. Young's Double-Slit Experiment (YDSE):

Monochromatic light(single wavelength or one-color light) is used.

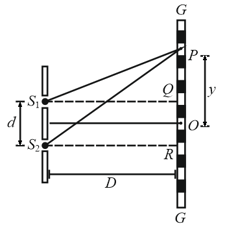
Here, d= distance between slits,

D= distance between slits and screen,

λ= wavelength of monochromatic light emitted from source

(i) Central fringe is bright, as at central position $\varphi =0°$or $\mathrm{\Delta }x=0$, where $\varphi =$phase difference, $∆x=$geaometrical path difference

(ii) If the slit widths are unequal, the minima will not be completely dark.

(iii) Geometrical path difference, $\mathrm{\Delta }x=S_{2}P-S_{1}P=d\sin \theta$, if $d\ll D$ or

$\mathrm{\Delta }x=\frac{\mathrm{d}y}{D}$ if $y\ll D$, where $\theta =$angle made by line ${\mathrm{S}}_1\mathrm{P}$ with the horizontal axis passing through $\mathrm{O}$

(a) for maxima, $\mathrm{\Delta }x=n\lambda$or $y=n\beta$, where $n=0, \pm 1, \pm 2...$ for central maxima

(b) for minima, $\mathrm{\Delta }x=\left(2n-1\right)\frac{\lambda }{2}$, where $n=\pm \mathrm{1,} \pm 2, \pm 3...$ or

y=2n-1β2, where fringe width β=λDd

(iv) Highest order maxima, $n_{\max }=\left[\frac{d}{\lambda }\right]$, where [ ] represents greatest integer function.

(v) Total number of maxima $=2n_{\max }+1$

(vi) Highest order minima, $n_{\max }=\left[\frac{d}{\lambda }+\frac{1}{2}\right]$, where [ ] represents greatest integer function.

(vii) Total number of minima $=2n_{\max }$

(viii) Intensity on screen, $I=I_1+I_2+2\sqrt{I_1{I}_2}\cos \left(\varphi \right)$, where $\varphi =\frac{2\mathrm{\pi }}{\lambda }\mathrm{\Delta }x$

(ix) If $I_1=I_2, I=4I_1{\cos }^2\left(\frac{\varphi }{2}\right)$ 

(x) The nearest point to central maxima where the bright fringes coincide, $y=n_1{\beta }_1=n_2{\beta }_2=\mathrm{LCM}$ of β1 and β2

(xi) The nearest point to central maxima where the two dark fringes coincide, $y=\left(n_1-\frac{1}{2}\right){\beta }_1=\left(n_2-\frac{1}{2}\right){\beta }_2$

(xii) Optical path difference

(a) $\mathrm{\Delta }{x}_{\mathrm{opt}}=\mu \mathrm{\Delta }x$

(b) $\varphi =\frac{2\mathrm{\pi }}{\lambda }\mathrm{\Delta }x=\frac{2\mathrm{\pi }}{{\lambda }_{\mathrm{vacuum}}}\mathrm{\Delta }{x}_{\mathrm{opt}}$, where $\mathrm{\Delta }{x}_{\mathrm{opt}}=\left(\mu -1\right)t$, $\lambda =$wavelength of the light in a medium, ${\lambda }_{\mathrm{vacuum}}=$wavelength of the light in vacuum

(xiii) In YDSE, if n1 fringes are visible in a field of view with light of wavelength λ1 while n2 with light of wavelength λ2 in the same field, then n1λ1=n2λ2

9. YDSE with Oblique Incidence:

In YDSE, ray is incident on the slit at an inclination of θ0 to the axis of symmetry.

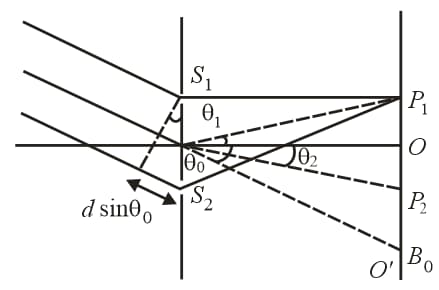
To get central maxima at a point, $\mathrm{\Delta }x=0$ when ${\theta }_2={\theta }_0$(at point $O$ in the diagram)

Path difference for different cases will be $\mathrm{\Delta }x=$

(i) $d\left(\sin {\theta }_0+\sin \theta \right)$for points above $O$

(ii) $d\left(\sin {\theta }_0-\sin \theta \right)$for points above O between $O\text{'}$

(iii) $d\left(\sin \theta -\sin {\theta }_0\right)$ for points below $O\text{'}$

10. Fringe Shift due to Glass Slab:

(i) Fringe shift $=\frac{D}{d}\left(\mu -1\right)\mathrm{t}=\frac{\mathrm{\beta }}{\mathrm{\lambda }}(\mu -1)\mathrm{t}$, where $\mu =$refractive index of the glass slab, $\beta =$fringe width, $t=$thickness of the glass slab

(ii) Additional path difference $=(\mu -1)\mathrm{t}$

(iii) Shift is independent of the order of fringe.

(iv) Shift is independent of wavelength.

11. Interference in Thin Films:

(i) Interference in reflected light:

(a) For constructive interference(maximum intensity), $\mathrm{\Delta }x=2\mu t\cos r=\left(2n-1\right)\frac{\lambda }{2}$, where $\mu =$refractive index of liquid film, $r=$angle of refraction when light enters from air to liquid film, $t=$thickness of the liquid film, $n=1, 2, 3,...$

For normal incidence $r = 0$ so $2\mu t=\left(2n-1\right)\frac{\lambda }{2}$

(b) For destructive interference (minimum intensity), $\mathrm{\Delta }x=2\mu t\cos r=\left(2n\right)\frac{\lambda }{2}$, for normal incidence $2\mu t=n\lambda$

(ii) Interference in refracted light:

(a) For constructive interference (maximum intensity case), $\mathrm{\Delta }x=2\mu t\cos r=\left(2n\right)\frac{\lambda }{2}$

For normal incidence $2\mu t=n\lambda$

(b) For destructive interference (minimum intensity case), $\mathrm{\Delta }=2\mu t\cos r=(2n-1)\frac{\lambda }{2}$

For normal incidence $2\mu t=\left(2n-1\right)\frac{\lambda }{2}$

12. Diffraction:

The bending of light around the corners of an obstacle/aperture of the size of the wavelength of light is called diffraction.

(i) Fresnel diffraction:

If either source or screen or both are at a finite distance from the diffracting device (obstacle or aperture), the diffraction is called Fresnel type. Diffraction at a straight edge, narrow wire or small opaque disc, etc.

(ii) Fraunhofer diffraction:

In this case, both source and screen are effectively at an infinite distance from the diffracting device.

Common examples: Diffraction at single slit, double slit and diffraction grating

13. Fraunhofer Diffraction:

The diffraction pattern consists of a central bright fringe (central maxima) surrounded by dark and brightlines (called secondary minima and maxima).

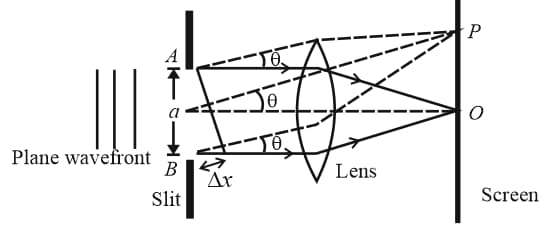
(i) For secondary minima, $a\sin \theta =n\lambda$, where $n=1, 2, 3 ...$

(ii) For secondary maxima, $a\sin \theta =(2n+1)\frac{\lambda }{2}$, where $n=1, 2, 3 ...$

(iii) Linear width of central maxima, $W_{\mathrm{x}}=\frac{2\lambda D}{a}$

(iv) Angular width of central maxima, $W_{\mathrm{\theta }}=\frac{2\lambda }{a}$

(v) Intensity of maxima, $I=I_0{\left[\frac{\sin (\beta /2)}{\frac{\beta }{2}}\right]}^2$, where I0= Intensity of central maxima and $\beta =\frac{2\pi }{\lambda }a\sin \theta$

14. Polarization:

Light propagates as transverse electromagnetic waves. The magnitude of electric field is much larger as compared to magnitude of magnetic field.

(i)

(a) Unpolarized light: Electric field vectors are distributed in all directions in ordinary lights.

(b) Polarized light: Electric field vector vibrates in one direction in a plane perpendicular to the direction of propagation of light.

(ii) Polarization by reflection

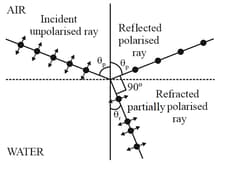
$\mu =\tan {\theta }_{\mathrm{p}}$, where ${\theta }_{\mathrm{p}}=$ Brewster's angle & ${\theta }_{\mathrm{p}}+{\theta }_{\mathrm{r}}=90°$(reflected and refracted rays are mutually perpendicular)

(iii) Polarization by scattering: Scattered light in the direction perpendicular to the direction of incident light is completely plane polarised while transmitted light is unpolarised. In all other directions, light is partially polarised.

(iv) Malus law:

The intensity of the polarised light transmitted through the analyzer varies as the square of the cosine of the angle between the plane of transmission of the analyzer and the plane of the polariser.

$I=I_0{\cos }^2\theta$

or $I=K{A}^2{\cos }^2\theta$, where $K=$constant

15. Resolving Power of Optical Instruments:

(i) Resolving power of telescope:

(a) The angular separation between two objects must be $\mathrm{\Delta }\theta$  $=\frac{1.22\mathrm{\lambda }}{d}$

(b) Resolving power $=\frac{1}{\mathrm{\Delta }\theta }=\frac{d}{1.22\mathrm{\lambda } }$

(ii) Resolving power of microscope:

(a) Distance between two objects that can be just resolved $=∆\mathrm{d}=\mathrm{ }\frac{\mathrm{\lambda }}{2n\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{ }\mathrm{\theta }}$

(b) Resolving power $=\frac{1}{∆\mathrm{d}}=\frac{2n\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{ }\mathrm{\theta }}{\mathrm{\lambda }}$

16. Doppler's Effect in Light:

Apparent change in frequency of the light due to relative motion between the source of light and the observer.

Given, $\nu =$ actual frequency,

ν'= apparent frequency,

$v=$ speed of source with respect to stationary observer,

c= speed of light

(i) Source moving towards observer:

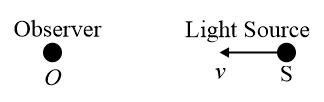
(a) Apparent frequency $\nu \text{'}=\left(\sqrt{\frac{1+\frac{v}{c}}{1-\frac{v}{c}}}\right)\nu \approx \left(1+\frac{v}{c}\right)\nu$ and apparent wavelength $\lambda \text{'}=\left(\sqrt{\frac{1-\frac{v}{c}}{1+\frac{v}{c}}}\right)\lambda \approx \left(1-\frac{v}{c}\right)\lambda$

(b) Spectrum of the radiation shifts towards the violet end of spectrum(violet shift).

(c) Doppler’s shift $\mathrm{\Delta }\mathrm{\lambda }=\mathrm{\lambda }\frac{\mathrm{v}}{\mathrm{c}}$

(ii) Source moving away from observer:

(a) Frequency $\nu \text{'}=\left(\sqrt{\frac{1-\frac{v}{c}}{1+\frac{v}{c}}}\right)\nu \approx \left(1-\frac{v}{c}\right)\nu$

(b) Wavelength $\lambda \text{'}=\left(\sqrt{\frac{1+\frac{v}{c}}{1-\frac{v}{c}}}\right)\lambda \approx \left(1+\frac{v}{c}\right)\lambda$

(c) Spectrum of the radiation shifts towards the red end of spectrum (red shift)

(iii) Application of Doppler effect:

(a) Determination of speed of airplane & submarine in Radar and Sonar

(b) Calculation of velocities of stars and galaxies by spectral shift

(c) Tracking of satellites