MEDIUM

JEE Main/Advanced

IMPORTANT

Earn 100

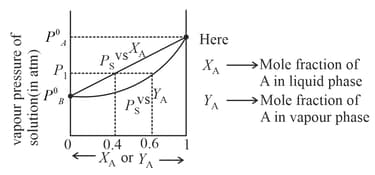
$A$ and $B$ are volatile liquid and form an ideal solution. Graph is given below in which upper dark line represent vapour pressure of solution and mole fraction of $A$ in liquid while lower dark line represent vapour pressure of solution and mole fraction of $A$ in vapour phase at temperature $T$ . Select the correct statement

33.33% studentsanswered this correctly

Important Points to Remember in Chapter -1 - Solutions from Embibe Experts Gamma Question Bank for Engineering Chemistry Solutions

1. Solution:

A homogeneous mixture of two or more non-reacting substances is known as solution, Homogeneity or heterogeneity depends upon particle size and states of matter present in the solution. Every solution is made up of a solvent (present in larger quantity) and one or more solute (present in smaller quantity).

2. Units of Concentration:

(i) Molarity $(M)$ :

It is the number of moles of solute present per litre of solution.

$M = \frac{n}{V} = \frac{W}{M_{w} V_{i n l i t r e}} = \frac{W}{M_{w}} \frac{1000}{V_{i n c c}}$

$M \times V_{i n c c} = \frac{W}{M_{w}} 1000$

$\Rightarrow M \times V (m L) =$ millimoles

Molarity changes with temperature of the solution. Increase in temperature generally decreases the molarity. It is the most convenient method to express concentration of the solution. On dilution, molarity decreases.

(ii) Molality $(m)$ :

Number of moles $(n)$ of solute present per $k g$ of solvent.

$m = \frac{n}{W_{i n k g}} = \frac{W}{M W_{i n k g}} = \frac{W}{M W_{i n g} s o l v e n t} 1000$

It is independent of temperature since no volume factor is involved in the equation.

(iii) Mole fraction $(X)$ :

It is the ratio of number of moles of one component to the total number of moles present in the solution.

For a system having two components $A$ and $B$ ,

$X_{A} = \frac{n_{A}}{n_{A} + n_{B}}, X_{B} = \frac{n_{B}}{n_{A} + n_{B}}$

$X_{A} + X_{B} = 1$

Mole fraction is also independent of temperature.

(iv) In terms of $%$

$%$ by weight $= \frac{W t . o f s o l u t e}{W t . o f s o l u t i o n} \times 100$

$%$ weight by volume $= \frac{W t . o f s o l u t e}{V o l . o f s o l u t i o n} \times 100$ (In case of solid dissolved in a liquid)

$%$ by volume $= \frac{V o l u m e o f s o l u t e}{V o l u m e o f s o l u t i o n} \times 100$ (In case of liquid dissolved in another liquid)

$P P M = \frac{N o . o f p a r t s o f s o l u t e}{N o . o f p a r t s o f s o l u t i o n} \times 10^{6}$

$%$ by weight is independent of temperature while $%$ by volume are temperature dependent.

3. Henry’ s Law:

Solubility of a gas at a given temperature in a solvent is directly proportional to its partial pressure, if $P$ is the partial pressure of a gas and $X_{g}$ is its mole fraction in solution. Then $P = K_{H} X_{g}$ , where $K_{H}$ is Henry's law constant for that gas.

4. Vapour Pressure and Raoult’s law:

The pressure exerted by the vapour at the free surface of liquid (provided system is closed) is known as its vapour pressure. The $V . P .$ of a pure liquid is always greater than its solution (in case of non-volatile solute).

(i) Raoult’s Law for a solution having non-volatile solute.

$X_{s o l u t e} = \frac{P^{\circ} - P_{s}}{P^{\circ}}$

$X_{s o l u t e} \to$ Mole fraction of solute in solution

$P^{\circ} \to V . P .$ of pure solvent

$P_{s} \to V . P .$ of solution

i.e., relative lowering of vapour pressure is equal to the mole fraction of solute.

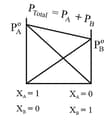
(ii) Raoult's Law of miscible liquid-liquid solution

For ideal solution, the partial vapour pressure is directly proportional to their mole fraction at constant temperature. For two components $A$ and $B$ in liquid solution.

$\Rightarrow P_{A} = P_{A}^{\circ} X_{A}$

$\Rightarrow P_{B} = P_{B}^{\circ} X_{B}$

The total pressure $P_{T o t a l} = P_{A} + P_{B} = P_{A}^{\circ} X_{A} + P_{B}^{\circ} X_{B}$

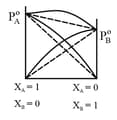
Question Image

Most of the solutions show appreciable deviations from ideal behavior known as real or non-ideal solution. In some cases, the deviation is $+ v e$ while in some cases deviation is $- v e$ .

5. Ideal and non-ideal Solutions:

The solutions which obey Raoult's law are ideal solutions and those which do not obey Raoult's law form non-ideal solution.

	Ideal Solution	Non-Ideal Solution
		Positive Deviation	Negative Deviation
1.	Obey Raoult's law	Disobey Raoult's law	Disobey Raoult's law
2.	$p_{A} = p_{A}^{\circ} X_{A}; p_{B} = p_{B}^{\circ} X_{B}$ $p_{T o t a l} = p_{A} + p_{B}$	$p_{A} > p_{A}^{\circ} X_{A}; p_{B} > p_{B}^{\circ} X_{B}$ $p_{T o t a l} = p_{A} + p_{B}$ $[p_{T o t a l} > P_{A} + P_{B}]$	$p_{A} < p_{A}^{\circ} X_{A}; p_{B} < p_{B}^{\circ} X_{B}$ $p_{T o t a l} = p_{A} + p_{B}$ $[p_{T o t a l} < P_{A} + P_{B}]$
3.	${Δ H}_{m i x} = 0$ ${Δ V}_{m i x} = 0$ ${Δ G}_{m i x} = - v e$ ${Δ S}_{m i x} = + v e$	${Δ H}_{m i x} = + v e$ ${Δ V}_{m i x} = + v e$ ${Δ G}_{m i x} = - v e$ ${Δ S}_{m i x} = + v e$	${Δ H}_{m i x} = - v e$ ${Δ V}_{m i x} = - v e$ ${Δ G}_{m i x} = - v e$ ${Δ S}_{m i x} = + v e$
4.	Interaction $A - B = A - A = B - B$ e.g., Chlorobenzene $+$ Bromobenzene	Interaction $A - B < A - A$ and $B - B$ e.g., ${C H}_{3} O H + H_{2} O$	Interaction $A - B > A - A$ and $B - B$ e.g., ${C H}_{3} {C O C H}_{3} + {C H C l}_{3}$
5.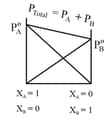

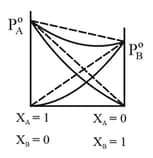6. Colligative Properties:

A colligative property of a solution is one that depends on the number of particles of solute in solution.

(i) Relative lowering of vapour pressure, $\frac{p - p_{s}}{p} = x_{s o l u t e}$ .

(ii) Osmotic pressure, $π = C R T$ .

(iii) Elevation of boiling point, ${∆ T}_{b} = k_{b} m$

(iv) Depression in freezing point, ${∆ T}_{f} = k_{f} m$ .

7. Relative Lowering of $V . P .$ :

The relative lowering in $V . P .$ of an ideal solution is equal to the mole fraction of solute at that temperature.

$\frac{p_{A}^{°} - p_{A}}{p_{A}^{°}} = x_{B} = \frac{n_{2}}{n_{1} + n_{2}}$

$\frac{n_{2}}{n_{1}} = (\frac{w_{2}}{M_{2}} \frac{M_{1}}{w_{1}})$ for dilute solutions.

Determination of molecular masses by relative lowering in vapour pressure.

$\frac{p_{A}^{°} - p_{A}}{p_{A}^{°}} = \frac{w}{m} \frac{M}{W}$

$w =$ Wt. of solute

$m =$ Mol. wt. of solute

$W =$ Wt. of solvent

$M =$ Mol. wt. of solvent

8. Osmotic Pressure:

(i) $π = ρ g h$

Where, $ρ =$ density of soln., $h =$ equilibrium height.

(ii) Van’t Hoff Formula (For calculation of $O . P .$ )

$π = C S T$

$π = C R T = \frac{n}{V} R T$ (just like ideal gas equation)

$∴ C =$ total conc. of all types of particles.

$= C_{1} + C_{2} + C_{3} +$

$= \frac{(n_{1} + n_{2} + n_{3} + \dots)}{V}$

Note: If $V_{1} m L$ of $C_{1}$ conc. $+ V_{2} m L$ of $C_{2}$ conc. are mixed

$π = (\frac{C_{1} V_{1} + C_{2} V_{2}}{V_{1} + V_{2}}) R T$

$π = (\frac{π_{1} V_{1} - π_{2} V_{2}}{V_{1} + V_{2}})$

9. Type of Solutions:

(i) Isotonic solution - Two solutions having same osmotic pressure.

$π_{1} = π_{2}$ (at same temp.)

(ii) Hypertonic - If $π_{1} > π_{2} \Rightarrow 1^{s t}$ solution is hypertonic solution w.r.t. $2^{n d}$ solution.

(iii) Hypotonic – If ${π_{1} > π_{2} \Rightarrow 2}^{n d}$ solution is hypotonic w.r.t. $1^{s t}$ solution.

10. Elevation of Boiling Point:

${∆ T}_{b} = k_{b} m$

Where, $K_{b}$ : Molal elevation constant or ebullioscopic constant, it is the increase in boiling point when the molality of the solution is unity.

${∆ T}_{b} = K_{b} m$ , when $m = 1$ , ${∆ T}_{b} = K_{b}$

$M_{B} = \frac{W_{B}}{{∆ T}_{b}} \frac{1000}{W_{A}} K_{b}$

$K_{b} = \frac{{M R T}_{b}^{2}}{1000 H_{v a p}}$

11. Depression in Freezing Point:

${∆ T}_{f} = k_{f} m$ .

Whdere, $K_{f} :$ Molal depression constant. or cryoscopic constant, it is the decrease in freezing point when the molality of solution is unity.

${∆ T}_{f} = K_{f} m$ when, $m = 1$ , ${∆ T}_{f} = K_{f}$

$M_{B} = \frac{K_{f} W_{B}}{{∆ T}_{f} W_{A}} 1000$

$K_{f} = \frac{{M R T}_{f}^{2}}{1000 H_{f u s i o n}}$

Note: $K_{b}$ and $K_{f}$ are intensive properties of solvent and do not depend upon the quantity and nature of solute.

12. Abnormal Molecular mass and Van't Hoff Factor $(i)$ :

$i = \frac{E x p e r i m e n t a l v a l u e s o f C o l l i g a t i v e p r o p e r t y}{C a l c u l a t e d v a l u e o f c o l l i g a t i v e p r o p e r t y}$

$= \frac{O b s e r v e d v a l u e o f C o l l i g a t i v e p r o p e r t y}{N o r m a l v a l u e o f t h e s a m e p r o p e r t y}$

$= \frac{N o r m a l m o l e c u l e r m a s s}{O b s e r v e d m o l e c u l e r m a s s}$

$= \frac{M_{c a l}}{M_{o b s}}$

Since Colligative property $\propto \frac{1}{M o l e c u l a r m a s s o f s o l u t e}$

if $i = 1$ , no molecular association or dissociation takes place.

if $i < 1$ , molecular association takes place.

if $i > 1$ , molecular dissociation takes place.

For substances undergoing association or dissociation in the solution.

$Δ T_{b} = i K_{b} m$

$Δ T_{f} = i K_{f} m$

$π = i C R T$

13. Relation between degree of association or dissociation $(α)$ & Van't Hoff's Factor $(i)$ :

For association $i = 1 + α (\frac{1}{n} - 1)$ or $α = \frac{n (i - 1)}{1 - n}$

where $n =$ Number of particles that associate.

For dissociation $i = 1 + α (n - 1)$ or $α = \frac{i - 1}{n - 1}$

where $n =$ Number of particles obtained on dissociation.

Important Points to Remember in Chapter -1 - Solutions from Embibe Experts Gamma Question Bank for Engineering Chemistry Solutions

Learn and Prepare for any exam you want !