A block is placed inside a horizontal hollow cylinder. The cylinder is rotating with a constant angular speed of one revolution per second about its axis. The angular position of the block at which it begins to slide is $30°$ below the horizontal level passing through the centre. Find the radius of the cylinder if the coefficient of friction is $0.6$. What should be the minimum constant angular speed of the cylinder so that the block reaches the highest point of the cylinder?

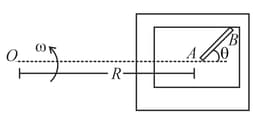
A table with the smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity $\omega$ in a circular path of radius $R$ (figure). A smooth groove $AB$ of length $L(\ll R)$ is made on the surface of the table. The groove makes an angle $\theta$ with the radius $OA$ of the circle in which the cabin rotates. A small particle is kept at the point $A$ in the groove and is released to move along $AB$. Find the time taken by the particle to reach the point $B$.

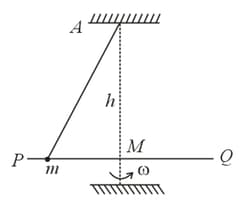
A smooth rod $PQ$ is rotated in a horizontal plane about its mid-point $M$ with height, $h=0.1 \mathrm{m}$ vertically below a fixed point $A$ at a constant angular velocity $14 \mathrm{rad} {\mathrm{s}}^{-1}$. A light elastic string of natural length $0.1 \mathrm{m}$ requiring $1.47 \mathrm{N} {\mathrm{cm}}^{-1}$ has one end fixed at $A$ and its other end attached to a ring of mass $m=0.3 \mathrm{kg}$ which is free to slide along the rod. When the ring is stationary relative to the rod, then find inclination of string with vertical, tension in string and force exerted by the ring on the rod $(g=9.8 \mathrm{m} {\mathrm{s}}^{-2})$.

A mass $m_1$ lies on fixed smooth cylinder. An ideal cord attached to $m_1$ passes over the cylinder and is connected to mass $m_2$ as shown in the figure.

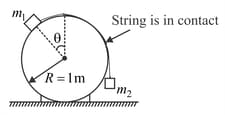
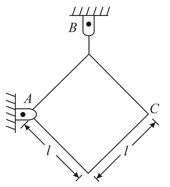
 Find the value of $\mathrm{\theta }$ in degree (shown in the diagram) for which the system is in equilibrium if $m_1=\sqrt{2} \mathrm{kg}$ and $m_2=1 \mathrm{kg}$.

A mass $m_1$ lies on fixed smooth cylinder. An ideal cord attached to $m_1$ passes over the cylinder and is connected to mass $m_2$ as shown in the figure.

 if $m_1=5 \mathrm{kg}, m_2=4 \mathrm{kg}$. The system is released from rest when $\mathrm{\theta }=30°$. Find the value of $N$ if the magnitude of the acceleration of mass $m_1$ just after the system is released is $\frac{N}{9} \mathrm{m} {\mathrm{s}}^{-2}$.

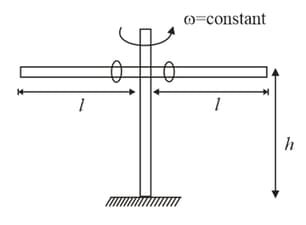
Two identical rings which can slide along the rod are kept near the midpoint of a smooth rod of length $2l(l=1 \mathrm{m})$ The rod is rotated with constant angular velocity $\omega =3 \mathrm{rad} {\mathrm{s}}^{-1}$ about the vertical axis passing through its center. The rod is at height $h=5 \mathrm{m}$ from the ground. Find the distance (in meter) between the points on the ground where the rings will fall after leaving the rods.

A table with the smooth horizontal surface is placed in a cabin which moves in a circle of a large radius $R$ (figure). A smooth pulley of a small radius is fastened to the table. Two masses $m$ and $2m$ placed on the table are connected through a string over the pulley. Initially, the masses are held by a person with the string along the outward radius and then the system is released from rest (with respect to the cabin). Find the value of $\frac{T}{ma}$, where $a$ is the magnitude of the initial acceleration of the masses as seen from the cabin and $T$ is the tension in the string.

A uniform square plate of mass m is supported as shown. If the cable suddenly breaks, determine just after that moment 

(a) The angular acceleration of the plate. 

(b) The acceleration of corner $C$.   

(c) The reaction at $A$.

Disk $A$ has a mass of $4 \mathrm{kg}$ and a radius $r=75 \mathrm{mm}$, it is at rest when it is placed in contact with the belt which moves at a constant speed $\nu =18 \mathrm{m} {\mathrm{s}}^{-1}.$ Knowing that ${\mu }_{\mathrm{k}}=0.25$ between the disk and the belt, determine the number of revolutions executed by the disk before it reaches a constant angular velocity. (Assume that the normal reaction by the belt on the disc is equal to weight of the disc). Take $g=10 \mathrm{m} {\mathrm{s}}^{-2}$