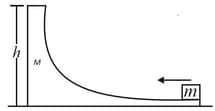
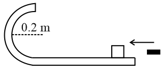
A bullet of mass moving horizontally at a speed of strikes a block of mass kept on a frictionless track as shown in figure. The bullet remains inside the block and the system proceeds towards the semicircular track of radius . Where will the block strike the horizontal part after leaving the semicircular track?


Important Questions on Centre of Mass, Linear Momentum, Collision
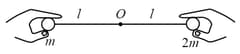
Two balls having masses and are fastened to two light strings of the same length . The other ends of the strings are fixed at . The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic.
Find the velocities of the balls just after their collision.
How high will the balls rise after the collision?
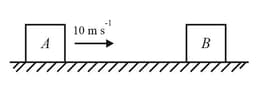
The blocks, shown in the figure, have equal masses. The surface of is smooth but that of has a friction coefficient of with the floor. Block is moving at a speed of towards which is kept at rest. Find the distance travelled by , if
(a) The collision is perfectly elastic and
(b) The collision is perfectly inelastic. Take .
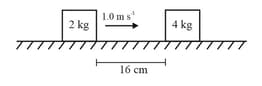
The friction coefficient between the horizontal surface and each of the blocks shown in the figure is . The collision between the blocks is perfectly elastic. Find the separation between the two blocks when they come to rest. Take .
A block of mass is placed on a triangular block of mass which in turn is placed on a horizontal surface, as shown in the figure. Assuming frictionless surfaces, find the velocity of the triangular block when the smaller block reaches the bottom end.
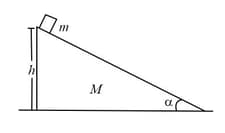
Figure shows a small body of mass placed over a larger mass , whose surface is horizontal near the smaller mass and gradually curves to become vertical. The smaller mass is pushed on the longer one at a speed and the system is left to itself. Assume that all the surfaces are frictionless.
(a) Find the speed of the larger block when the smaller block is sliding on the vertical part.
(b) Find the speed of the smaller mass when it breaks off the larger mass at height .
(c) Find the maximum height (from the ground) that the smaller mass ascends.
(d) Show that the smaller mass will again land on the bigger one. Find the distance traversed by the bigger block during the time when the smaller block was in its flight under gravity.