A car is moving with a speed of $10 \mathrm{m} {\mathrm{s}}^{-1}$ on a circular path of radius $25 \mathrm{m}$. Driver of car applies the brakes producing a uniform deceleration of$3 \mathrm{m} {\mathrm{s}}^2$. Then,
A) The centripetal acceleration of car just after applying the brake is 4 m/s².
B) The acceleration just after applying the brake is 5 m/s².
C) The acceleration is directed towards the centre just after applying the brake.
D) The angle between acceleration and velocity just after applying the brake is 127.

A clock has a continuously moving second's hand of $0.1 \mathrm{m}$ length. The average acceleration of the tip of the hand (in units of $\mathrm{m} {\mathrm{s}}^{-2}$) is of the order of :

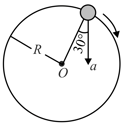
In the given figure, $a=15 \mathrm{m} {\mathrm{s}}^{-2}$ represents the total acceleration of a particle moving in the clockwise direction in a circle of the radius $R=2.5 \mathrm{m}$at a given instant of time. The speed of the particle is

A mass $\text{m}$ moves in a circle on a smooth horizontal plane with velocity ${\mathrm{v}}_0$ at a radius ${\mathrm{R}}_0$ . The mass is attached to a string which passes through a smooth hole in plane as shown.

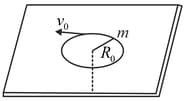
The tension in the string is increased gradually and finally $\text{m}$ moves in a circle of radius $\frac{{\mathrm{R}}_0}{2}$. The final value of the kinetic energy is:

If the kinetic energy of a particle of mass $m,$ performing uniform circular motion in a circle of radius $r,$ is $E,$ find the acceleration of the particle.