A circle intersects a hexagon such that the area of the hexagon outside the circle is the same as the area of the circle outside the hexagon. If each side of the hexagon is $\mathrm{a}$, what is the area of the circle?

There are two congruent squares placed in such a way that the sides of one square are parallel to the diagonals of the other square, whereas the point of intersection of diagonals of one square coincides with that of the diagonals of the other. There is a circle passing through the points of intersection of sides of the two square. And there is another circle passing through the vertices of the two squares. If each side of the square is $2+\sqrt{2}$ unit, find the ratio of the area of the smaller circle to that of the larger circle.

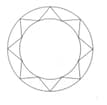
In the following figure find the ratio of the area of the internal hexagon to that of the external regular hexagon.

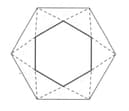
In the following figure find the ratio of the shaded triangular area to that of the remaining area of the regular hexagon.

In the following diagram, as shown below, a regular hexagon of side $3 \mathrm{cm}$ inscribes $7$ smaller regular hexagons. Find the area of the shaded region (of the triangles) within the larger hexagon.

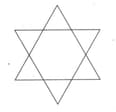
In the following figure a hexagram consists of a hexagon and six equilateral triangles outside the hexagon. If a circle is inscribed in the hexagon and the area of the inscribed circle is $3\mathrm{\pi }$ $\mathrm{sq}.$ $\mathrm{cm}$, find the area of the circumscribed circle of the regular hexagram.

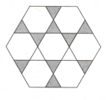
In the following hexagonal ring the area of shaded region is $3$ times the area of the un-shaded region. Find the ratio of perimeter of the outer hexagon to that of the inner hexagon.