A circular loop of string rotates about its axis on a frictionless horizontal plane at a uniform rate so that the tangential speed of any particle of the string is $v$. If a small transverse disturbance is produced at a point of the loop, with what speed (relative to the string) will this disturbance travel on the string?

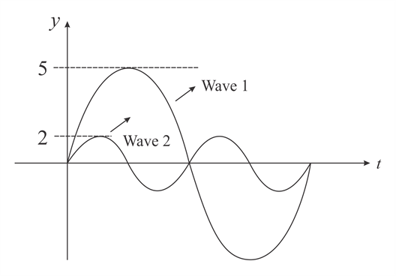
Two waves in the same medium are represented by $y-t$ curves in the figure. Find the ratio of their average intensities?

A sinusoidal wave on a string is described by the wave function$y=(0.15 \mathrm{m})\sin (0.80x-50t)$ where $x$ and $y$ are in metres and $t$ is in seconds. The mass per unit length of this string is $12.0 \mathrm{g} {\mathrm{m}}^{-1}$. Determine the power transmitted to the wave.

A sinusoidal wave on a string is described by the wave function$y=(0.15 \mathrm{m})\sin (0.80x-50t)$ where $x$ and $y$ are in metres and $t$ is in seconds. The mass per unit length of this string is $12.0 \mathrm{g}/\mathrm{m}$. Determine

the speed of the wave,

A sinusoidal wave on a string is described by the wave function, $y=(0.15 \mathrm{m})\sin (0.80x-50t)$ where $x$ and $y$ are in metres and $t$ is in seconds. The mass per unit length of this string is $12.0 \mathrm{g} {\mathrm{m}}^{-1}$. Determine the frequency. 

A transverse harmonic wave is propagating along a taut string. Tension in the string is $50 \mathrm{N}$ and its linear mass density is $0.02 \mathrm{kg}{ \mathrm{m}}^{-1}$. The string is driven by a $80 \mathrm{Hz}$ oscillator tied to one end oscillating with an amplitude of $2 \mathrm{mm}$. The other end of the string is terminated so that all the wave energy is absorbed and there is no reflection. Calculate the power of the oscillator.