A cylindrical capacitor is constructed using two coaxial cylinders of the same length and of radii and .
(a) Calculate the capacitance.
(b) Another capacitor of the same length is constructed with cylinders of radii and . Calculate the capacitance.
(a) Calculate the capacitance.
(b) Another capacitor of the same length is constructed with cylinders of radii and . Calculate the capacitance.

Important Points to Remember in Chapter -1 - Capacitors from H C Verma CONCEPTS OF PHYSICS [VOLUME 2] Solutions
1. Capacitor & capacitance:
(i) A capacitor consists of two conductors carrying charges of equal magnitude and opposite sign.
(ii) The capacitance of any capacitor is the ratio of the charge on either conductor to the potential difference between them .
(iii) The capacitance depends only on the geometry of the conductors and not on an external source of charge or potential difference.
2. Dielectric:
Dielectrics are insulating (non-conducting) materials that transmit electric effects without conducting.
Dielectrics are of two types.
3. Polar dielectrics:
A polar molecule has a permanent electric dipole moment in the absence of an electric field also. But a polar dielectric has a net dipole moment zero in the absence of an electric field because polar molecules are randomly oriented as shown in the figure.
4. Nonpolar dielectric:
(i) In non-polar molecules, each molecule has zero dipole moment in its normal state.
(ii) When an electric field is applied, molecules become induced electric dipoles e.g., , Benzene, Methane, etc. are made of non-polar atoms/molecules.
5. Dielectric breakdown and dielectric strength:
(i) If a very high electric field is created in a dielectric, the dielectric then behaves like a conductor. This phenomenon is known as a dielectric breakdown.
(ii) The maximum value of electric field (or potential gradient) that a dielectric material can tolerate without its electric breakdown is called its dielectric strength.
(iii) S.I. unit of dielectric strength of a material is but the practical unit is .
6. Parallel plate capacitor:
(i) , where, charge on positive plate of the capacitor, Capacitance of capacitor and, Potential difference between positive and negative plates.
(ii) Capacitance, , where is surface area of plate and d is the distance between the plates.
(iii) When complete space between the plates is occupied by a medium of dielectric constant K, then .
(iv) Electric field between the plates:
(v) Energy density between the plates of the capacitor,
(vi) Representation of capacitor:
(vii) Attractive force between the capacitor plates,
7. Capacitor with dielectric:
(i) Capacitance in the presence of dielectric:
(a)
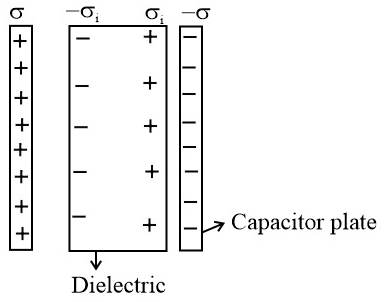
Capacitance in the absence of dielectric.
(b)
(c) Electric field in the absence of dielectric.
(d) Field inside the slab is
(e)
(f) Induced (bound) charge density.
8. Capacitance with different dielectrics:
(i) If a dielectric slab is partially filled between the plates
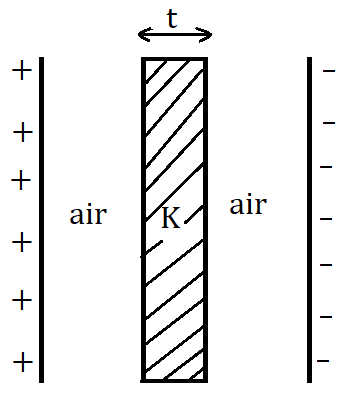
Note: for metal plate inside the capacitor, . So,
(ii) Capacitor with multiple dielectrics:
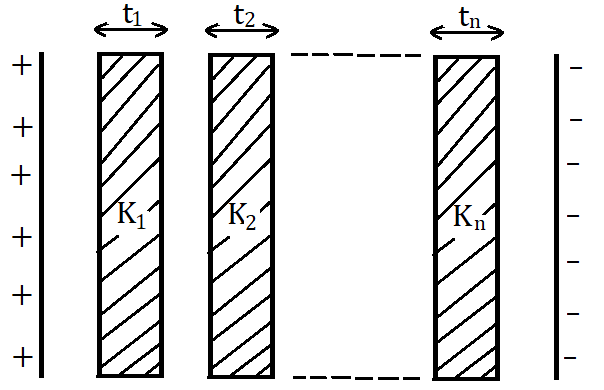
(iii) Capacitor with three different dielectrics:
(a) Case I:
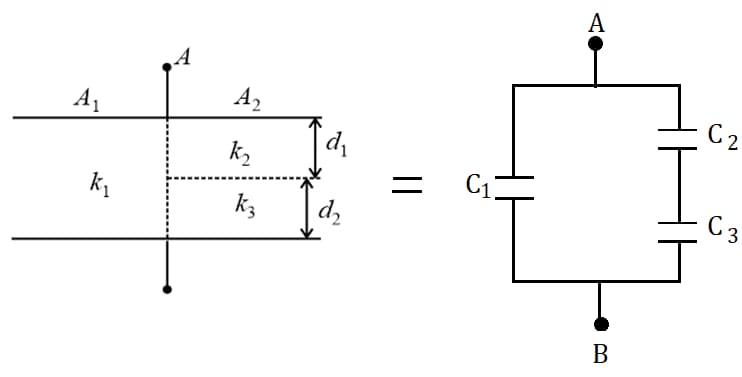
, and
The effective capacitance of the combination is, .
(b) Case II:
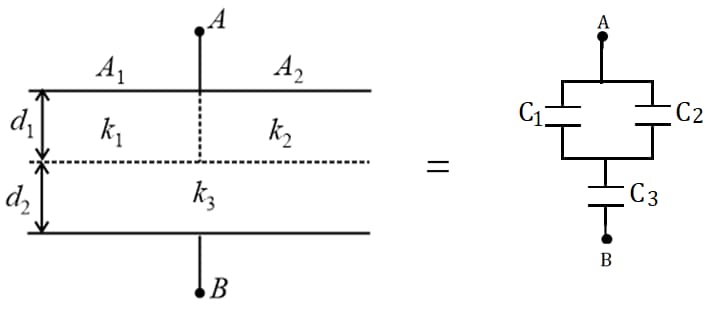
, and
The effective capacitance is,
9. Capacitance of an Isolated Spherical Conductor:
(i) in a medium
(ii) in air
10. Spherical Capacitor:
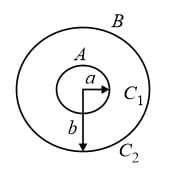
It consists of two concentric spherical shells as shown in the figure. Here capacitance of the region between the two shells is and that outside the shell is . We have
and
(i) Case I: If the outer shell is earthed, then the capacitance
(ii) Case II: If the inner shell is earthed, then and will be in parallel.
So, the effective capacitance becomes
(iii) Case III: If there exists a potential difference between inner shell and infinity, then and will be in series.
11. Cylindrical capacitor: It consists of two concentric cylinders of radii and , inner cylinder is given charge +Q while the outer cylinder is earthed. The common length of the cylinders is then
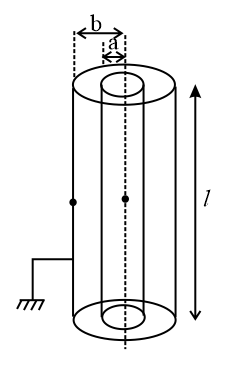
12. Energy stored in the capacitor:
(i)
(ii) Energy density . Where, Relative permittivity of the medium, dielectric Constant.
(iii) For vacuum, energy density
(iv) In charging a capacitor by battery half the energy supplied is stored in the capacitor and the remaining half energy is lost in the form of heat.
13. Effect of dielectric on the energy stored in a capacitor:
(i) Case I: Keeping the battery connection if a dielectric is inserted between the plates of a capacitor such that the gap is completely occupied, then the energy becomes
(ii) Case II: Keeping the charge constant if a dielectric is inserted between the plates of a capacitor such that the gap is completely occupied, then the energy becomes,
14. Heat Produced in a capacitive circuit:
Heat Work done by battery change in potential energy of capacitors.
(i) Case 1:
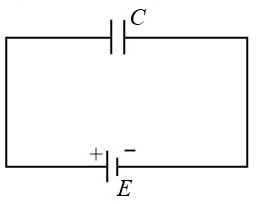
In the given figure, the heat lost on reversing the terminals of the battery is,
(ii) Case 2:
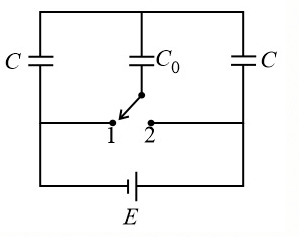
In the given figure, the heat lost when the switch is shifted from 1 to 2 is
15. Combination of capacitors:
(i) Series Combination:
(a) Charge on all capacitors is the same.
(b)
(c)
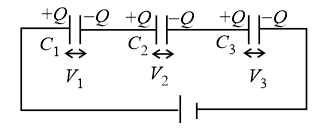
(ii) Parallel Combination:
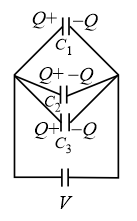
(a) Potential difference is the same across all capacitors.
(b)
(c)
16. Coalesce of charged drops:
Suppose we have identical drops each having radius , capacitance , charge , potential and potential energy .
If these drops are combined to form a big drop of radius , capacitance , charge , potential and potential energy , then
(i) Charge on big drop:
(ii) Radius of big drop: Volume of big drop volume of a single drop
i.e., ,
(iii) Capacitance of big drop:
(iv) Potential of big drop:
(v) Energy of big drop:
(vi) Energy difference: Total energy of big drop is greater than the total energy of all smaller drops. Hence energy difference
17. Distribution of charges on connecting two charged capacitors:
When two capacitors are and are connected as shown in figure
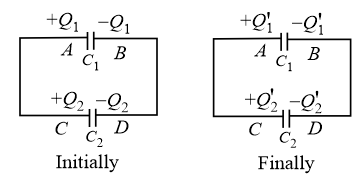
(i) Common potential:
(ii)
(iii)
(iv) Heat loss during redistribution:
.
The loss of energy is in the form of Joule heating in the wire.
18. Force on dielectric:
(i) When the battery is connected
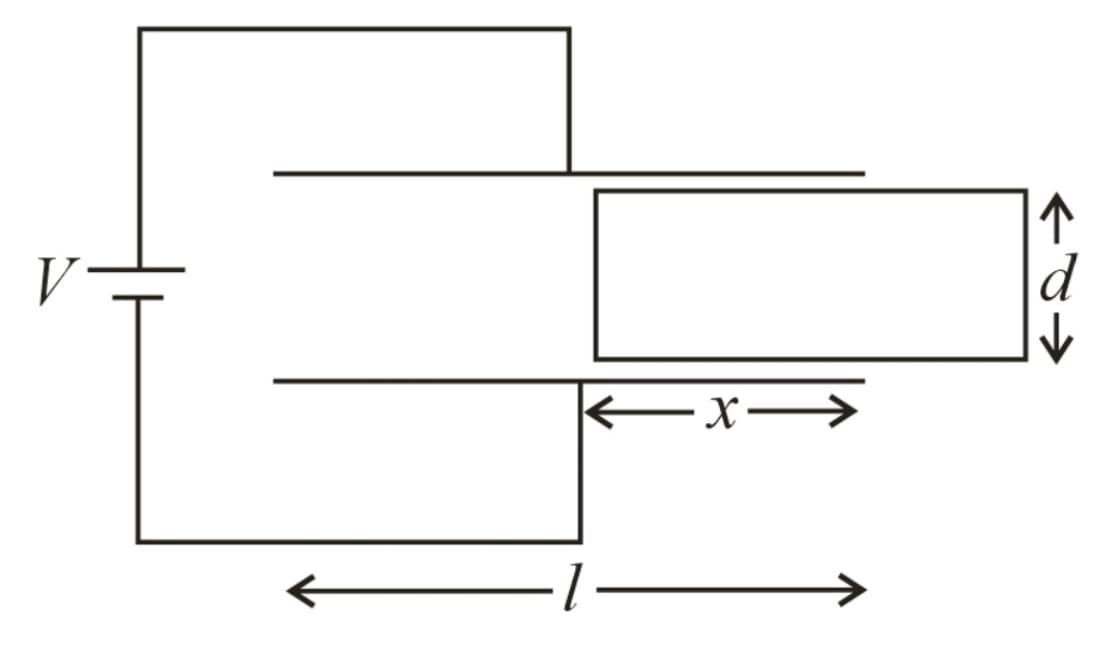
Note that the force is constant and independent of .
(ii) When the battery is not connected
i.e., . Where, is the width of the plate or dielectric slab.
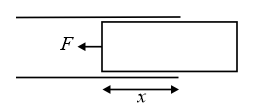
(iii) Force on the dielectric will be zero when the dielectric is fully inside.
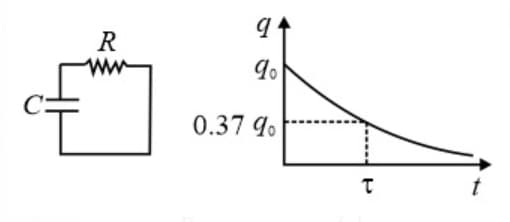
19. R-C circuit for DC source:
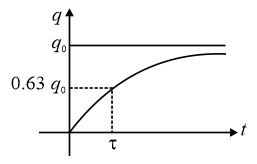
(i) Charging of Capacitor:
(a) Charge on Capacitor (Capacitor initially uncharged)
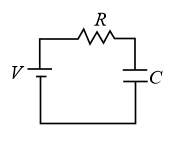
Charge on the capacitor at steady state
(b)
(c) Time constant
(d)
(ii) Discharging of Capacitor:
(a)
Initial charge on the capacitor
(b)