A cylindrical layer of dielectric with permittivity, is inserted into a cylindrical capacitor to fill up all the space between the electrodes. The mean radius of the electrodes equals $R$, the gap between them is equal to $d$, with $d\ll R$. The constant voltage $V$ is applied across the electrodes of the capacitor. Find the magnitude of the electric force pulling the dielectric into the capacitor.

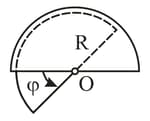
A capacitor consists of two stationary plates shaped as a semi-circle of radius $R$, and a movable plate made of a dielectric with permittivity $\epsilon$, and capable of rotating about an axis $O$ between the stationary plates (figure). The thickness of the movable plate is equal to $d$, which is practically the separation between the stationary plates. A potential difference $V$ is applied to the capacitor. Find the magnitude of the moment of forces relative to the axis $O$, acting on the movable plate in the position shown in the figure.

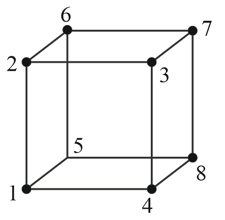
Find the resistance of a wire frame shaped as a cube (figure) when measured between points:
(a) $1-7$; (b) $1-2$; (c) $1-3$. The resistance of each edge of the frame is $R$.

At what value of the resistance $R_{\mathrm{x}}$, in the circuit shown in the figure, will the total resistance between points $A$ and $B$ be independent of the number of cells?

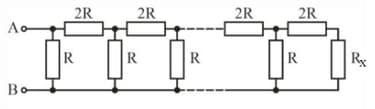
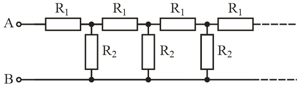
Figure shows an infinite circuit formed by the repetition of the same link, consisting of resistances $R_1=4.0 \mathrm{\Omega }$ and $R_2=3.0 \mathrm{\Omega }$. Find the resistance of this circuit between points $A$and $B$.

The gap between the plates of a parallel-plate capacitor is filled with glass of resistivity $\rho =100 \mathrm{G\Omega } \mathrm{m}$. The capacitance of the capacitor equals $C=4.0 \mathrm{nF}$. Find the leakage current of the capacitor, when a voltage $V=2.0 \mathrm{kV}$ is applied to it. (Permittivity of vacuum, ${\epsilon }_0=0.885\times {10}^{-11} \mathrm{F} {\mathrm{m}}^{-1}$, $\epsilon =$ Dielectric constant for glass $=6$)