A fair six-sided die has the digits $1,2,3,4,5,6$ on its faces.

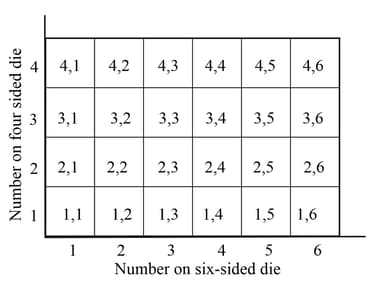
A fair four-sided die has the digits $1,2,3,4$ on its faces.

The two dice are rolled simultaneously. The diagram represents the sample space of the possible outcomes.

Let $A$ be the event 'rolling a $1$ on the four-sided die', and $B$ be the event 'rolling a $1$ on the six-sided die. Find $P\left(A\cap B\right)$, the probability that you roll a $1$ on the four-sided die and a $1$ on the six-sided die.

A fair six-sided die has the digits $1,2,3,4,5,6$ on its faces.

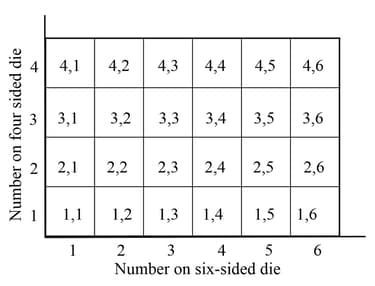
A fair four-sided die has the digits $1,2,3,4$ on its faces.

The two dice are rolled simultaneously. The diagram represents the sample space of the possible outcomes.

Let $A$ be the event 'rolling a $1$ on the four-sided die', and $B$ be the event 'rolling a $1$ on the six-sided die. Explain whether or not the events are independent.

A fair six-sided die has the digits $1,2,3,4,5,6$ on its faces.

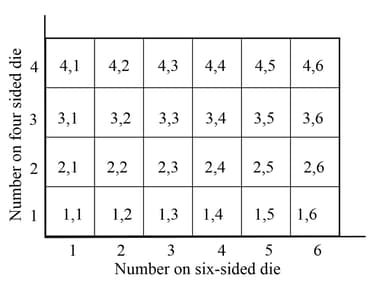
A fair four-sided die has the digits $1,2,3,4$ on its faces.

The two dice are rolled simultaneously. The diagram represents the sample space of the possible outcomes.

Let $A$ be the event 'rolling a $1$ on the four-sided die', and $B$ be the event 'rolling a $1$ on the six-sided die. Explain whether or not the events are independent. Verify your result using the multiplication rule.

A red die has faces numbered $1,2,3,4,5,6$ and a green die has faces numbered $0,0,1,1,2,$ and $2$. Let $A$ be the event 'rolling a $2$ on the red die'. Let $B$ be the event 'rolling a $2$ on the green die'. Calculate the probability of rolling a $2$ on both the red die and the green die.

A red die has faces numbered $1,2,3,4,5,6$ and a green die has faces numbered $0,0,1,1,2,$ and $2$. Let $A$ be the event 'rolling a $2$ on the red die'. Let $B$ be the event 'rolling a $2$ on the green die'. Calculate the probability of rolling a $2$ on both the red die and the green die. Explain whether or not these events are independent.

A red die has faces numbered $1,2,3,4,5,6$ and a green die has faces numbered $0,0,1,1,2,$ and $2$. Let $A$ be the event 'rolling a $2$ on the red die'. Let $B$ be the event 'rolling a $2$ on the green die'. Calculate the probability of rolling a $2$ on both the red die and the green die. Explain whether or not these events are independent. Verify your result using the multiplication rule.

Here is a standard set of dominos.

One domino is selected at random. It is then replaced and a second domino is drawn at random. If $S$ is the set of outcomes of selecting $2$ dominos, write down $n\left(S\right)$.

Here is a standard set of dominos.

One domino is selected at random. It is then replaced and a second domino is drawn at random. If $S$ is the set of outcomes of selecting $2$ dominos, write down $n\left(S\right)$. Let $A$ be the event 'at least one of the values on the first domino is a six' and $B$ be the event 'the second domino is a double' (both values are the same). Explain whether or not these events are independent.

Here is a standard set of dominos.

One domino is selected at random. It is then replaced and a second domino is drawn at random. If $S$ is the set of outcomes of selecting $2$ dominos, write down $n\left(S\right)$. Let $A$ be the event 'at least one of the values on the first domino is a six' and $B$ be the event 'the second domino is a double' (both values are the same). Explain whether or not these events are independent. Verify your answer using the multiplication rule.