EASY
12th CBSE
IMPORTANT
Earn 100
A long charged cylinder of linear charge density is surrounded by a hollow coaxial conducting cylinder of linear charge density . Use Gauss’s law to obtain expression for the electric field at a point in the space between the cylinders.

Important Questions on Electrostatic Potential and Capacitance
EASY
12th CBSE
IMPORTANT
A long charged cylinder of linear charge density is surrounded by a hollow coaxial conducting cylinder of linear charge density . Use Gauss’s law to obtain expression for the electric field at a point outside the larger cylinder.
MEDIUM
12th CBSE
IMPORTANT
Find the expression for the electric field intensity and the electric potential, due to a dipole at a point on the equatorial line. Would the electric field be necessarily zero at a point where the electric potential is zero? Give an example to illustrate your answer.
MEDIUM
12th CBSE
IMPORTANT
Obtain the expression for the potential due to a point charge.
MEDIUM
12th CBSE
IMPORTANT
Use the above expression to show that the potential, due to an electric dipole (length ), varies as the ‘inverse square’ of the distance of the ‘field point’ from the centre of the dipole for .
HARD
12th CBSE
IMPORTANT
Define the term electric dipole moment. Derive an expression for the total work done in rotating the dipole through an angle in the uniform electric field .
MEDIUM
12th CBSE
IMPORTANT
Derive an expression for the potential energy of an electric dipole placed in a uniform electric field. Hence discuss the conditions of its stable and unstable equilibrium.
EASY
12th CBSE
IMPORTANT
Explain why, for any charge configuration, the equipotential surface through a point is normal to the electric field at that point.
Draw a sketch of equipotential surfaces due to a single charge , depicting the electric field lines due to the charge.
EASY
12th CBSE
IMPORTANT
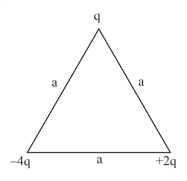
Obtain an expression for the work done to dissociate the system of three charges placed at the vertices of an equilateral triangle of side as shown here.