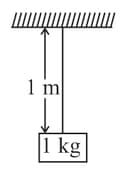
A one meter long massless string fixed with a wall is pulled horizontally by applying a force of magnitude $10 \mathrm{N}$. Calculate:

(a) the tension at a point $0.5 \mathrm{m}$ away from wall, 

(b) the tension at a point $0.75 \mathrm{m}$ away from wall, 

(c) force exerted by string on the rigid support.

A block of mass $1 \mathrm{kg}$ is suspended by a string of mass $1 \mathrm{kg}$, length $1 \mathrm{m}$ as shown in the figure $(g=10 \mathrm{m} {\mathrm{s}}^{-2})$. Calculate:

(a) the tension in string at its lowest point, 

(b) the tension in string at its mid-point, 

(c) force exerted by support on string.

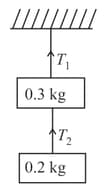
A block of mass $0.3 \mathrm{kg}$ is suspended from the ceiling by a light string. A second block of mass $0.2 \mathrm{kg}$ is suspended from the first block through another string. Find the tensions in the two strings. Take $g=10 \mathrm{m} {\mathrm{s}}^{-2}$.

Two unequal masses $m_1$ and $m_2$ are connected by a string going over a clamped light smooth pulley as shown in figure $m_1=3 \mathrm{kg}$ and $m_2=6 \mathrm{kg}$. The system is released from rest. (a) Find the distance travelled by the first block in the first two seconds. (b) Find the tension in the string. (c) Find the force exerted by the clamp on the pulley. $(g=10 \mathrm{m} {\mathrm{s}}^{-2})$

A mass $M$ is held in place by an applied force $F$ and a pulley system as shown in the figure. The pulleys are massless and frictionless.

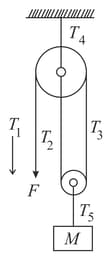
(a) Draw a free body diagram for each pulley.

(b) Find the tension in each section of rope $T_1, T_2, T_3, T_4$ and $T_5$.

(c) Find the magnitude of $F$.

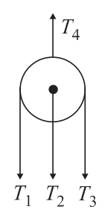
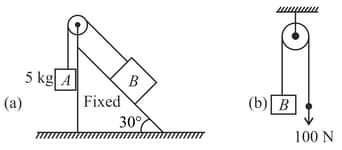
In the figure, the tension in the string between the points $1$ and $2$ is $60 \mathrm{N}$.

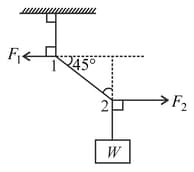
(a) Find the magnitude of the horizontal force ${\mathrm{F}}_1$ and ${\mathrm{F}}_2$ which must be applied to hold the system according to the position shown in figure.

(b) What is the weight of the suspended block?

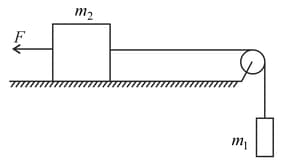
A constant force $F=m_{1}g/2$ is applied on the block of mass $m_2$ as shown in the figure. The string and the pulley are light and the surface of the table is smooth. Find the acceleration of $m_2$.

 A chain consisting of five links each with mass $100 \mathrm{gm}$ is lifted vertically with constant acceleration of $2 \mathrm{m} {\mathrm{s}}^{-2}$ $\left(\uparrow \right)$ as shown. Find $(g=10 \mathrm{m} {\mathrm{s}}^{-2})$

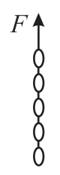
(a) the forces acting between adjacent links.

(b) the force $F$ exerted on the top link by the agent lifting the chain.

(c) the net force on each link.

Find out the mass of block $B$ to keep the system at rest $(g=10 \mathrm{m} {\mathrm{s}}^{-2})$.