A particle moves up a line of greatest slope of a rough plane inclined at an angle $\alpha$ to the horizontal, where $\sin \alpha =0.28.$ The coefficient of friction between the particle and the plane is $\frac{1}{3}.$

Show that the acceleration of the particle is $-6 \mathrm{m}{\mathrm{s}}^{-2}.$

A particle moves up a line of greatest slope of a rough plane inclined at an angle $\alpha$ to the horizontal, where $\sin \alpha =0.28.$ The coefficient of friction between the particle and the plane is $\frac{1}{3}.$

Given that the particle's initial speed is $5.4 \mathrm{m}{\mathrm{s}}^{-1},$ find the distance that the particle travels up the plane.

A block of weight$7.5 \mathrm{N}$ is at rest on a plane which is inclined to the horizontal at angle $\alpha ,$ where $\tan \alpha =\frac{7}{24}.$ The coefficient of friction between the block and the plane is $\mu .$ A force of magnitude $7.2 \mathrm{N}$ acting parallel to a line of greatest slope is applied to the block. When the force acts up the plane (see Fig. $1$) the block remains at rest.

Show that $\mu ⩾\frac{17}{24}$.

When the force acts down the plane (see Fig. $2$) the block slides downwards.

A block of weight$7.5 \mathrm{N}$ is at rest on a plane which is inclined to the horizontal at angle $\alpha ,$ where $\tan \alpha =\frac{7}{24}.$ The coefficient of friction between the block and the plane is $\mu .$ A force of magnitude $7.2 \mathrm{N}$ acting parallel to a line of greatest slope is applied to the block. When the force acts up the plane (see Fig. $1$) the block remains at rest.

Show that $\mu <\frac{31}{24}.$

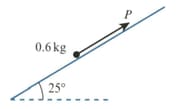
The diagram shows a particle of mass $0.6 \mathrm{kg}$ on a plane inclined at $25°$ to the horizontal. The particle is acted on by a force of magnitude $P \mathrm{N}$ directed up the plane parallel to a line of greatest slope. The coefficient of friction between the particle and the plane is $0.36.$ Given that the particle is in equilibrium, find the set of possible values of $P$