HARD

JEE Main

IMPORTANT

Earn 100

A particle of unit mass undergoes one dimensional motion such that its velocity varies according to $v (x) = {bx}^{- 2 n}$ , where b and n are constants and $x$ is the position of the particle. The acceleration of the particle as the function of $x$ , is given by:

50% studentsanswered this correctly

Important Questions on Kinematics

MEDIUM

JEE Main

IMPORTANT

Physics Crash Course JEE Main>Chapter 2 - Kinematics>Level 3>Q 2

A ball is thrown vertically upwards. It was observed at a height

h

, twice with a time interval

∆ t

. The initial velocity of the ball is

HARD

JEE Main

IMPORTANT

Physics Crash Course JEE Main>Chapter 2 - Kinematics>Level 3>Q 3

A particle moving along x-axis has acceleration f , at time t , given by $f = f_{0} (1 - \frac{t}{T})$ , where $f_{0}$ and T are constants. The particle at $t = 0$ has zero velocity. In the time interval between $t = 0$ and the instant when $f = 0$ , the change in particle’s velocity $(v_{x})$ is

HARD

JEE Main

IMPORTANT

Physics Crash Course JEE Main>Chapter 2 - Kinematics>Level 3>Q 4

A ball of mass $m$ is thrown upward with a velocity $v$ . The air exerts an average resisting force $F$ . The velocity with which the ball returns to the thrower is

HARD

JEE Main

IMPORTANT

Physics Crash Course JEE Main>Chapter 2 - Kinematics>Level 3>Q 5

Two towns

A

and

B

are connected by a regular bus service with a bus leaving in either direction every

T \min

with same speed. A man cycling with speed of

20 km h^{- 1}

in the direction

A

B

, notices that a bus goes past him every

t_{1} = 18 \min

in the direction of motion, and every

t_{2} = 6 \min

in the opposite direction. What is the period

T

of the bus service? Assume that the velocity of cyclist is less than velocity of bus.

HARD

JEE Main

IMPORTANT

Physics Crash Course JEE Main>Chapter 2 - Kinematics>Level 3>Q 6

Three particles

A, B

and

C

simultaneously start from the origin. Particle

A

moves with a velocity

a

along

X -

axis, particle

B

moves with a velocity

b

along

Y -

axis and particle

C

moves with a velocity

c

in the

X - Y

plane along the straight line

x = y

. The magnitude of

c

so that all the three particles always remain collinear is

EASY

JEE Main

IMPORTANT

Physics Crash Course JEE Main>Chapter 2 - Kinematics>Level 3>Q 7

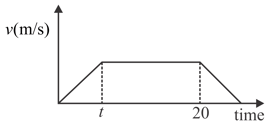
The velocity-time graph of a particle moving along a straight line is as shown in the diagram. The rate of acceleration and retardation is constant and is equal to $5 m s^{- 2}$ . If the average velocity during the motion is $20 m s^{- 1},$ then the maximum velocity of the particle is

Question Image

EASY

JEE Main

IMPORTANT

Physics Crash Course JEE Main>Chapter 2 - Kinematics>Level 3>Q 8

Initially car

A

10.5 m

ahead of car

B

. Both start moving at time

t = 0

in the same direction along a straight line. The velocity time graph of two cars is shown in figure. Find the time (in

s

) when the car

B

will catch the car

A

, will be:
Question Image

HARD

JEE Main

IMPORTANT

Physics Crash Course JEE Main>Chapter 2 - Kinematics>Level 3>Q 9

The velocity displacement graph of a particle moving along a straight line is shown.

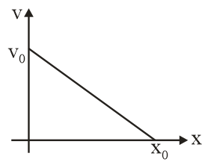
Question Image

The most suitable acceleration-displacement graph will be

A particle of unit mass undergoes one dimensional motion such that its velocity varies according to v(x)=bx-2n, where b and n are constants and x is the position of the particle. The acceleration of the particle as the function of x, is given by:

Important Questions on Kinematics

Learn and Prepare for any exam you want !

A particle of unit mass undergoes one dimensional motion such that its velocity varies according to $v (x) = {bx}^{- 2 n}$ , where b and n are constants and $x$ is the position of the particle. The acceleration of the particle as the function of $x$ , is given by: