MEDIUM

Earn 100

A particle performing SHM has time period $\frac{2 π}{\sqrt{3}}$ and path length 4 cm. The displacement from mean position at which acceleration is equal to velocity is

47.27% studentsanswered this correctly

Important Questions on Oscillations

MEDIUM

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion

In an engine the piston undergoes vertical simple harmonic motion with amplitude 7cm. A washer rests on top of the piston and moves with it. The motor speed is slowly increased. The frequency of the piston at which the washer no longer stays in contact with the piston, is close to :

EASY

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion

A particle executes linear simple harmonic motion with an amplitude of 3 cm. When the particle is at 2 cm from the mean position, the magnitude of its velocity is equal to that of its acceleration. Then its time period in seconds is

MEDIUM

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion

Two particles are performing simple harmonic motion in a straight line about the same equilibrium point. The amplitude and time period for both particles are same and equal to

A

and

T

, respectively. At time

t = 0

one particle has displacement

A

while the other one has displacement

- \frac{A}{2}

and they are moving towards each other. If they cross each other at time

t

, then

t

is:

EASY

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion

A particle is executing a simple harmonic motion. Its maximum acceleration is

α

and maximum velocity is

β

. Then, its time period of vibration will be:

MEDIUM

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion

The position co-ordinates of a particle moving in a $3 D$ coordinate system is given by

$x = a \cos ω t$

$y = a \sin ω t$

and $z = a ω t$

The speed of the particle is:

EASY

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion

The oscillation of a body on a smooth horizontal surface is represented by the equation,

X = A \cos (ω t)

, where

X =

displacement at time

t

ω =

frequency of oscillation,

a =

acceleration at time

t

and

T =

time period.
Which one of the following graph shows correctly the variation

a

with

t

MEDIUM

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion

A particle performs simple harmonic motion with amplitude A. Its speed is tripled at the instant that it is at a distance

\frac{2 A}{3}

from equilibrium position. The new amplitude of the motion is:

MEDIUM

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion

The phase difference between displacement and acceleration of a particle in a simple harmonic motion is:

HARD

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion

A particle executes simple harmonic motion with an amplitude of

5 cm

. When the particle is at

4 cm

from the mean position, the magnitude of its velocity in

SI

units is equal to that of its acceleration. Then, its periodic time in seconds is:

HARD

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion

A particle performs linear SHM. At a particular instant, the velocity of the particle is

u

and acceleration is

α

(both having the same direction). At another instant velocity is

v

and acceleration is

β (0 < α < β)

(both in opposite direction to each other).The distance between the two positions is

HARD

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion

A particle is performing a linear simple harmonic motion of amplitude

A

. When it is midway between its mean and extreme position, the magnitudes of its velocity and acceleration are equal. What is the periodic time of the motion?

EASY

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion

A particle is executing SHM along a straight line. Its velocities at distances

x_{1}

and

x_{2}

from the mean position are

V_{1}

and

V_{2}

respectively. Its time period is:

HARD

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion

A piston is performing

S . H . M .

in the vertical direction with a frequency of

0.5 Hz

. A block of

10 kg

is placed on the piston. The maximum amplitude of the system such that the block remains in contact with the piston is

EASY

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion

The radius of circle, the period of revolution, initial position and sense of revolution are indicated in the figure.
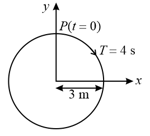
Question Image

y

-projection of the radius vector of rotating particle

P

MEDIUM

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion

The displacement time graph of a particle executing SHM is given in figure: (sketch is schematic and not to scale)

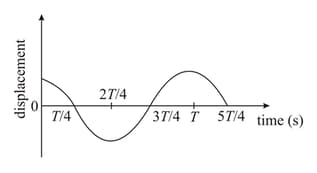
Question Image

Which of the following statements is/are true for this motion?

(A) The force is zero at $t = \frac{3 T}{4}$
(B) The magnitude of acceleration is maximum at $t = T$
(C) The speed is maximum at $t = \frac{T}{4}$
(D) The $P . E .$ is equal to $K . E .$ of the oscillation at $t = \frac{T}{2}$

EASY

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion

A simple pendulum oscillates harmonically about

x = 0

with an amplitude

A

and time period

T

. Its speed at

x = A / 2

EASY

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion

If the differential equation for a simple harmonic motion is

\frac{d^{2} y}{d t^{2}} + 2 y = 0

, the time period of the motion is,

HARD

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion

The ratio of maximum acceleration to maximum velocity in a simple harmonic motion is

10 s^{- 1} .

At,

t = 0

the displacement is

5 m .

What is the maximum acceleration? The initial phase is

\frac{π}{4}

EASY

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion

A particle is performing SHM starting from extreme position. Graphical representation shows that, between displacement and acceleration, there is a phase difference of

EASY

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion

Which of the following plots represents schematically the dependence of the time period of a pendulum if measured and plotted as a function of its oscillations? (Note: amplitude need not be small)

A particle performing SHM has time period 2π3 and path length 4 cm. The displacement from mean position at which acceleration is equal to velocity is

Important Questions on Oscillations

Learn and Prepare for any exam you want !

A particle performing SHM has time period $\frac{2 π}{\sqrt{3}}$ and path length 4 cm. The displacement from mean position at which acceleration is equal to velocity is