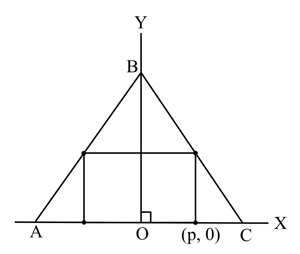
A rectangle is inscribed in isosceles triangle as shown in the diagram.The altitude of triangle from to side is cm and cm. The coordinates of one of the vertices of the inscribed rectangle are . Find the dimensions of the rectangle inscribed in the triangle, in terms of .


Important Questions on Modelling Relationships: Linear and Quadratic Functions
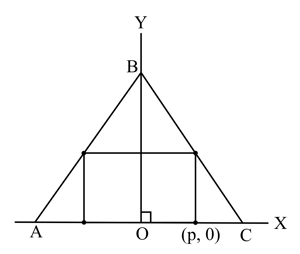
A rectangle is inscribed in isosceles triangle as shown in the diagram.The altitude of triangle from to side is cm and cm. The coordinates of one of the vertices of the inscribed rectangle are . Write down an expression for the area of the inscribed rectangle in terms of .
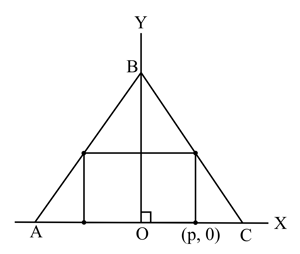
A rectangle is inscribed in isosceles triangle as shown in the diagram.The altitude of triangle from to side is cm and cm. The coordinates of one of the vertices of the inscribed rectangle are . Find the dimensions of the rectangle with maximum possible area..
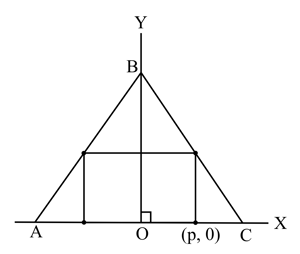
A rectangle is inscribed in isosceles triangle as shown in the diagram.The altitude of triangle from to side is cm and cm. The coordinates of one of the vertices of the inscribed rectangle are . Find the maximum possible area of the inscribed rectangle.