A ring of mass $m$ and radius $r$ is rotated in uniform magnetic field $B$ which is perpendicular to the plane of the loop with constant angular velocity ${\omega }_0$. Find the net ampere force on the ring and the tension developed in the ring if there is a current i in the ring. Current and rotation both are clockwise.

A point charge $q=2\mathrm{\mu C}$ is at the origin. It has velocity $2\hat{\mathrm{i}} \mathrm{m} {\mathrm{s}}^{-1}$. Find the magnetic field at the following points in vector form (at the moment when the charged particle passes through the origin):

(i) $\left(2, 0, 0\right)$

(ii) $\left(0, 2, 0\right)$

(iii) $\left(0, 0, 2\right)$

(iv) $\left(2, 1, 2\right)$

(v) Is the magnitude of the magnetic field on the circumference of the circle (in $yz$ plane) $y^2+z^2=c^2$, where $c$ is a constant is same everywhere. Is it same in direction also?

(vi) Answer the above (v) for the circle of same equation but in a plane $x=a$, where $a$ is a constant.

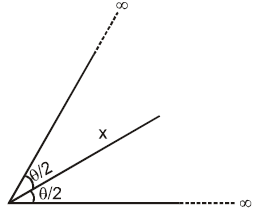
A long wire carrying a current $i$ is bent to form a plane angle $\theta$. Find the magnetic field $B$ at a point on the bisector of this angle situated at a distance $x$ from the vertex is written in the form of $K\cot \frac{\theta }{4} \mathrm{T}$. Then, find the value of $K$.

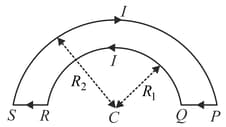
Two wire loops $\mathrm{PQRSP}$ formed by joining two semicircular wires of radii $R_1$ and $R_2$ carries a current $I$ as shown in (figure). The magnitude of the magnetic induction at the center $\mathrm{C}$ is 

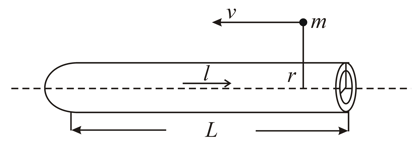
A thin but long and hollow cylindrical tube of radius $r$ carries a current $i$ along its length. Find the magnitude of the magnetic field at a distance $r/2$ from the surface:

$\left(\mathrm{a}\right)$ inside the tube.

$\left(\mathrm{b}\right)$ outside the tube.

A long non-magnetic cylindrical conductor with inner radius a and outer radius $\mathrm{b}$ carries a current $\mathrm{I}$. The current density in the conductor is uniform. Assume end effects can be neglected.

(a) Prove by the Biot-Savart law that the magnetic field, if any, at a point is always tangential to the circle passing through the point, with the centre of the circles on the axis of the cylinder.

(b) Find the magnetic field due to the current as a function of radius.

(i) inside the hollow space $(\mathrm{r} < \mathrm{a})$ (ii) within the conductor $(\mathrm{a} < \mathrm{r} < \mathrm{b})$(iii) outside the conductor $(\mathrm{r} > \mathrm{b})$

(c) A beam of particles, each with positive charge $\mathrm{q}$ and mass $\mathrm{m}$ travels with initial velocity $\mathrm{v}$ anti-parallel to the direction of the current. Assume that the length of cylinder is $\mathrm{L}$. Find the deflection of a particle as a function of its initial distance r from the axis if $\mathrm{r} > \mathrm{b}$ when it goes from one end to other end. You can assume that the velocity is high enough such that the velocity is constant and the deflection is small.