HARD
Earn 100
A rocket has to be launched from earth in such a way that it never returns. If E is the minimum energy delivered by the rocket launcher, what should be the minimum energy that the launcher should have if the same rocket is to be launched from the surface of the moon ? Assume that the density of the earth and the moon are equal and that the earth's volume is the volume of the moon.
(a)
(b)
(c).
(d)
50% studentsanswered this correctly
Important Questions on Gravitation
HARD
MEDIUM
EASY
EASY
MEDIUM
MEDIUM
MEDIUM
MEDIUM
[If, and radius of earth ]
MEDIUM
MEDIUM
EASY
use
MEDIUM
MEDIUM
MEDIUM
MEDIUM
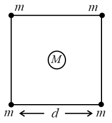
Four spheres each of mass form a square of side (as shown in figure). A fifth sphere of mass is situated at the centre of square. The total gravitational potential energy of the system is
MEDIUM
MEDIUM
(Take radius of earth and )
HARD
MEDIUM
MEDIUM

