MEDIUM
Earn 100
A rod of mass ' ' and length ' ' lying on a frictionless horizontal surface is initially given an angular velocity ' ' about vertical axis with centre of mass at rest, but circular motion is not fixed. Subsequently end of rod collides with nail , which is near to such that end becomes stationary immediately after impact. Velocity of end '' just after collision will be -
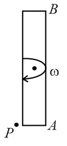
(a)
(b)
(c)
(d)
50% studentsanswered this correctly
Important Questions on Systems of Particles and Rotational Motion
HARD
A particle of mass m is moving along the side of a square of side 'a', with a uniform speed in the x-y plane as shown in the figure:
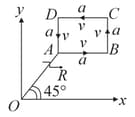
Which of the following statements is false for the angular momentum about the origin?
EASY
A solid sphere is rotating freely about its symmetric axis in free space. The radius of the sphere is increased keeping its mass same. Which of the following physical quantities would remain constant for the sphere?
EASY
A ball of mass is thrown up at an angle of to the horizontal at a speed of . The angular momentum of the ball at the highest point of the trajectory with respect to the point from which the ball is thrown is nearly
MEDIUM
Two coaxial discs, having moments of inertia and , are rotating with respective angular velocities and (in the same direction), about their common axis. They are brought in contact with each other and thereafter they rotate with a common angular velocity. If and are the final and initial total energies, then is:
MEDIUM
A bob of mass m attached to an inextensible string of length is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed rad/s about the vertical. About the point of suspension :
MEDIUM
The time dependence of the position of a particle of mass is given by . Its angular momentum, with respect to the origin, at time is:
HARD
A horizontal disk of moment of inertia with respect to its axis of symmetry is spinning counter clockwise at revolutions per second about its axis, as viewed from above. A second disk of moment of inertia with respect to its axis of symmetry is spinning clockwise at revolutions per second as viewed from above about the same axis and is dropped on top of the first disk. The two disks stick together and rotate as one about their axis of symmetry. The new angular velocity of the system as viewed from above is close to.
EASY
A particle is moving uniformly along a straight line as shown in the figure. During the motion of the particle from to , the angular momentum of the particle about
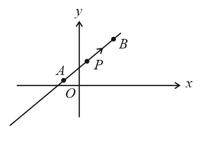
EASY
Two rotating bodies, and of masses, and with moments of inertia and have equal kinetic energy of rotation. If, and be their angular momenta, respectively, then,
HARD
A disc of the moment of inertia is rotating in a horizontal plane about an axis passing through a centre and perpendicular to its plane with constant angular speed Another disc of the moment of inertia having zero angular speed is placed coaxially on a rotating disc. Now both the disc are rotating with the constant angular speed . The energy lost by the initial rotating disc is
MEDIUM
A thin smooth rod of length and mass is rotating freely with angular speed about an axis perpendicular to the rod and passing through center. Two beads of mass and negligible size are at the center of the rod initially. The beads of mass and negligible size are at the center of the rod initially. The beads are free to slide along the rod. The angular speed of the system, when the beads reach the opposite ends of the rod, will be:
HARD
A hoop of radius and mass rotating with an angular velocity is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it ceases to slip?
HARD
Three point masses each of mass are kept at the corners of an equilateral triangle of side . The system rotates about the center of the triangle without any change in the separation of masses during rotation. The period of rotation is directly proportional to
MEDIUM
A cubical block of side is moving with velocity on a smooth horizontal surface. The surface has a bump at a point as shown in the figure. The angular velocity (in rad/s) of the block immediately after it hits the bump, is :
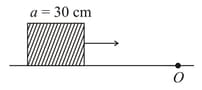
HARD
A uniformly thick wheel with moment of inertia and radius is free to rotate about its centre of mass (see fig). A massless string is wrapped over its rim and two blocks of masses and are attached to the ends of the string. The system is released from rest. The angular speed of the wheel when descends by a distance is:
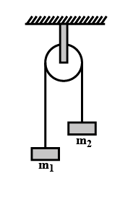
MEDIUM
Two uniform circular discs are rotating independently in the same direction around their common axis passing through their centres. The moment of inertia and angular velocity of the first disc are and respectively while those for the second one are and respectively. At some instant they get stuck together and start rotating as a single system about their common axis with some angular speed. The kinetic energy of the combined system is :
MEDIUM
A solid sphere of radius is revolving about one of its diameters with an angular velocity If it suddenly expands uniformly so that its radius increases to times its original value, then its angular velocity becomes
EASY
A thin circular ring of mass and radius is rotating about its axis perpendicular to the plane of the ring with a constant angular velocity . Two point particles each of mass are attached gently to the opposite ends of a diameter of the ring. The ring now rotates, with an angular velocity . Then, the ratio is
MEDIUM
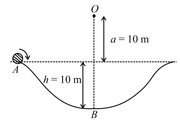
A particle of mass is on a smooth horizontal table and moves in a circular path of radius . The height of the table from the ground is . If the angular speed of the particle is , the magnitude of its angular momentum about a point on the ground right under the center of the circle is:
HARD
A particle of mass is released with an initial velocity along the curve from the point as shown in the figure. The point is at height from point The particle slides along the frictionless surface. When the particle reaches point its angular momentum about will be: (Take )