MEDIUM

Earn 100

A solid cylinder, a solid sphere, a hollow sphere and a hollow cylinder, all of same mass and diameter are released from the same height at the same time on an inclined plane. If all the bodies roll down without slipping, then the body which will reach the bottom first, is

50% studentsanswered this correctly

Important Questions on Rotational Mechanics

EASY

Physics>Mechanics>Rotational Mechanics>Pure Rolling

In a physical balance working on the principle of moments, when

5 mg

weight is placed on the left pan, the beam becomes horizontal. Both the empty pans of the balance are of equal mass. Which of the following statements is correct?

EASY

Physics>Mechanics>Rotational Mechanics>Pure Rolling

A solid sphere of mass,

m

and radius,

R

is rotating about its diameter. A solid cylinder of the same mass and same radius is also rotating about its geometrical axis with an angular speed twice that of the sphere. The ratio of their kinetic energies of rotation

(\frac{E_{sphere}}{E_{cylinder}})

will be

MEDIUM

Physics>Mechanics>Rotational Mechanics>Pure Rolling

A uniform disc of radius

R

and mass

M

is free to rotate only about its axis. A string is wrapped over its rim and a body of mass

m

is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is:

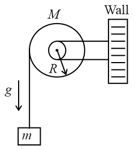
Question Image

MEDIUM

Physics>Mechanics>Rotational Mechanics>Pure Rolling

Consider a cylinder of mass M resting on a rough horizontal rug that is pulled out from under it with acceleration 'a' perpendicular to the axis of the cylinder. What is F_friction at point P ? It is assumed that the cylinder does not slip.
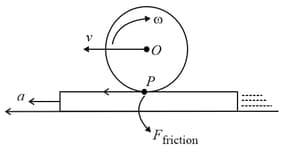
Question Image

MEDIUM

Physics>Mechanics>Rotational Mechanics>Pure Rolling

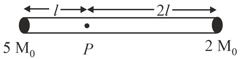
A rigid massless rod of length $3 l$ has two masses attached at each end as shown in the figure. The rod is pivoted at point $P$ on the horizontal axis. When released from the initial horizontal position, its instantaneous angular acceleration will be

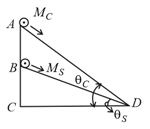
Question Image

HARD

Physics>Mechanics>Rotational Mechanics>Pure Rolling

A cylinder of mass M_c and sphere of mass M_s are placed at points A and B of two inclines, respectively. (See figure). If they roll on the incline without slipping such that their accelerations are the same, then the ratio

\frac{sin θ_{c}}{sin θ_{s}}

is :

EASY

Physics>Mechanics>Rotational Mechanics>Pure Rolling

A solid sphere of mass

2 kg

is rolling on a frictionless horizontal surface with velocity

6 m s^{- 1}

. It collides on the free end of an ideal spring whose other end is fixed. The maximum compression produced in the spring will be (Force constant of the spring =

36 N m^{- 1}

MEDIUM

Physics>Mechanics>Rotational Mechanics>Pure Rolling

A stationary horizontal disc is free to rotate about its axis. When a torque is applied on it, its kinetic energy as a function of

θ

, where

θ

is the angle by which it has rotated, is given as

k θ^{2}

. If its moment of inertia is

I

then the angular acceleration of the disc is:

MEDIUM

Physics>Mechanics>Rotational Mechanics>Pure Rolling

A homogeneous solid cylindrical roller of radius

R

and mass

M

is pulled on a cricket pitch by a horizontal force. Assuming rolling without slipping, angular acceleration of the cylinder is:

MEDIUM

Physics>Mechanics>Rotational Mechanics>Pure Rolling

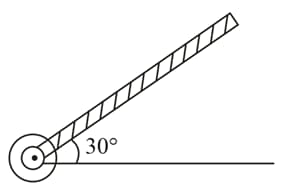
A rod of length $50 c m$ is pivoted at one end. It is raised such that it makes an angle of $30^{o}$ from the horizontal as shown and released from rest. Its angular speed when it passes through the horizontal (in $r a d s^{- 1}$ ) will be $(g = 10 m s^{- 2})$

Question Image

MEDIUM

Physics>Mechanics>Rotational Mechanics>Pure Rolling

A roller is made by joining together two cones at their vertices O. It is kept on two rails AB and CD which are placed asymmetrically (see figure), with its axis perpendicular to CD and its centre O at the centre of line joining AB and CD (see figure). It is given a light push so that it starts rolling with its centre O moving parallel to CD in the direction shown. As it moves, the roller will tend to:

Question Image

EASY

Physics>Mechanics>Rotational Mechanics>Pure Rolling

A uniform circular disc of radius

50 cm

at rest is free to rotate about an axis which is perpendicular to its plane and passes through its centre. It is subjected to a torque which produces a constant angular acceleration of

2.0 r a d s^{- 2}

. Its net acceleration in

m s^{- 2}

at the end of

2.0 s

is approximately:

EASY

Physics>Mechanics>Rotational Mechanics>Pure Rolling

A disc of radius

2 m

and mass

100 k g

rolls on a horizontal floor. Its centre of mass has speed of

20 c m s^{- 1} .

How much work is needed to stop it?

EASY

Physics>Mechanics>Rotational Mechanics>Pure Rolling

Two discs of same moment of inertia

(I)

are rotating in same sense about their regular axis passing through centre and perpendicular to the plane of disc with angular velocities

ω_{1}

and

ω_{2}

. They are brought into contact face to face coinciding the axis of rotation. The expression for loss in energy during this process is

MEDIUM

Physics>Mechanics>Rotational Mechanics>Pure Rolling

A solid sphere and solid cylinder of identical radii approach an incline with the same linear velocity (see figure). Both roll without slipping all throughout. The two climb maximum heights $h_{s p h}$ and $h_{c y l}$ on the incline. The ratio $\frac{h_{s p h}}{h_{c y l}}$ is given by:
Question Image

MEDIUM

Physics>Mechanics>Rotational Mechanics>Pure Rolling

The following bodies are made to roll up (without slipping) the same inclined plane from a horizontal plane: (i) a ring of radius

R,

(ii) a solid cylinder of radius

\frac{R}{2}

and (iii) a solid sphere of radius

\frac{R}{4} .

If, in each case, the speed of the center of mass at the bottom of the incline is same, the ratio of the maximum heights they climb is:

MEDIUM

Physics>Mechanics>Rotational Mechanics>Pure Rolling

The ratio of the acceleration for a solid sphere (mass

‘ m'

and radius

R)

rolling down an incline of angle

‘ θ'

without slipping and slipping down the incline without rolling is:

HARD

Physics>Mechanics>Rotational Mechanics>Pure Rolling

A uniform solid cylindrical roller of mass

m

is being pulled on a horizontal surface with force

F

parallel to the surface and applied at its centre. If the acceleration of the cylinder is

a

and it is rolling without slipping then the value of

F

is:

EASY

Physics>Mechanics>Rotational Mechanics>Pure Rolling

A disk and a sphere of same radius but different masses roll off on two inclined planes of the same altitude and length. Which one of the two objects gets to the bottom of the plane first?

EASY

Physics>Mechanics>Rotational Mechanics>Pure Rolling

A particle of mass

10 g

moves along a circle of radius

6.4 cm

with a constant tangential acceleration. What is the magnitude of this acceleration if the kinetic energy of the particle becomes equal to

8 \times 10^{- 4} J

by the end of the second revolution after the beginning of the motion?

A solid cylinder, a solid sphere, a hollow sphere and a hollow cylinder, all of same mass and diameter are released from the same height at the same time on an inclined plane. If all the bodies roll down without slipping, then the body which will reach the bottom first, is

Important Questions on Rotational Mechanics

Learn and Prepare for any exam you want !