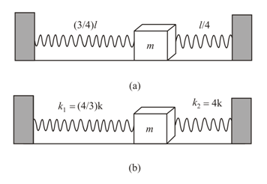
A spring of stiffness constant and natural length is cut into two parts of length and respectively, and an arrangement is made as shown in Figs. (a) and (b). If the mass is slightly displaced, find the time period of oscillation.


Important Questions on Linear and Angular Simple Harmonic Motion
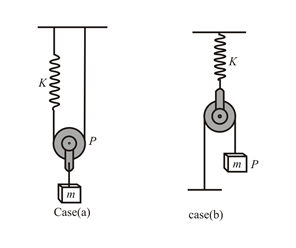
A block of mass hangs from a smooth light pulley and by an inextensible string fitted a spring of stiffness as shown in case and case
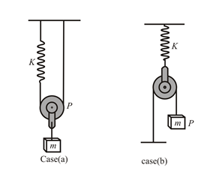
A block of mass hangs from a smooth light pulley and by an inextensible string fitted a spring of stiffness as shown in case and case
Find the period of oscillation of the block.
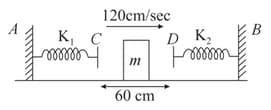
Two light springs of force constants and and a block of mass are in one line on a smooth horizontal table such that one end of each spring is fixed to rigid supports and the other end is free as shown in the figure. The distance between the free ends of the spring is . If the block moves along with a velocity in between the springs, calculate the period of oscillation of the block .
A particle of mass connected with a spring of force constant is executing simple harmonic motion with amplitude When it is at from equilibrium position moving towards right, it receives an impulse which doubles its velocity without changing direction.
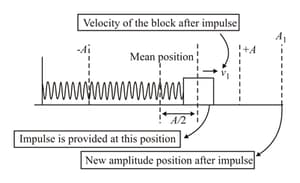
velocity of the particle after the impulse,
A particle of mass connected with a spring of force constant is executing simple harmonic motion with amplitude When it is at from equilibrium position moving towards right, it receives an impulse which doubles its velocity without changing direction.
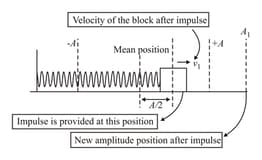
amplitude after the impulse, and
A particle of mass connected with a spring of force constant is executing simple harmonic motion with amplitude When it is at from equilibrium position moving towards the right, it receives an impulse which doubles its velocity without changing direction.
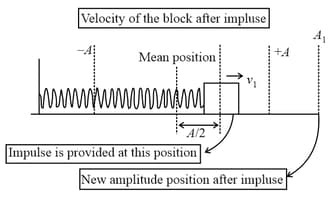
time taken by the block to reach the right extreme position.
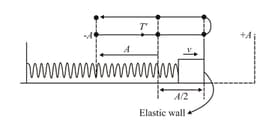
A block of mass connected to a spring of force constant is performing simple harmonic motion. Initially, the block is compressed by a distance and released. An elastic wall is located in front of block at a distance of Find the time period of oscillation of this block.
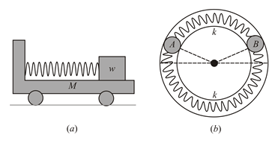
Figures (a) represent spring-block system. If $m$ is displaced slightly, find the time period of oscillation of the system.
Both the cases are as follows:
