HARD

Earn 100

A thin uniform rod of length $1$ m and mass $1$ kg is rotating about an axis passing through its centre and perpendicular to its length. Calculate the moment of inertia and radius of gyration of the rod about an axis passing through a point midway between the centre and its edge, perpendicular to its length.

Important Questions on Systems of Particles and Rotational Motion

MEDIUM

Physics>Mechanics>Systems of Particles and Rotational Motion>Moment of Inertia

A circular hole of radius

\frac{R}{4}

is made in a thin uniform disc having mass and radius

R

, as shown in figure. The moment of inertia of the remaining portion of the disc about an axis passing through the point

O

and perpendicular to the plane of the disc is-
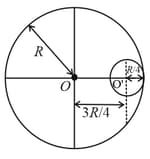
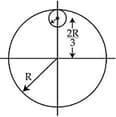
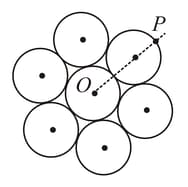
Question Image

MEDIUM

Physics>Mechanics>Systems of Particles and Rotational Motion>Moment of Inertia

The moment of inertia of a thin uniform rod of length

L

and mass

M

about an axis passing through a point at a distance of

\frac{L}{3}

from one of its ends and perpendicular to the rod is

EASY

Physics>Mechanics>Systems of Particles and Rotational Motion>Moment of Inertia

The moment of inertia of a uniform cylinder of length

l

and radius

R

about its perpendicular bisector is

I .

What is the ratio

l / R

such that the moment of inertia is minimum?

HARD

Physics>Mechanics>Systems of Particles and Rotational Motion>Moment of Inertia

From a uniform circular disc of radius R and mass 9 M, a small disc of radius

\frac{R}{3}

is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is:

Question Image

MEDIUM

Physics>Mechanics>Systems of Particles and Rotational Motion>Moment of Inertia

From a solid sphere of mass

M

and radius

R

, a cube of the maximum possible volume is cut. Moment of inertia of cube about an axis passing through its centre and perpendicular to one of its faces is:

HARD

Physics>Mechanics>Systems of Particles and Rotational Motion>Moment of Inertia

Seven identical circular planar disks, each of mass M and radius R are welded symmetrically as shown. The moment of inertia of the arrangement about the axis normal to the plane and passing through the point P is:
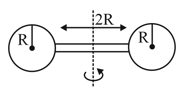
Question Image

HARD

Physics>Mechanics>Systems of Particles and Rotational Motion>Moment of Inertia

A uniform solid cylindrical roller of mass

m

is being pulled on a horizontal surface with force

F

parallel to the surface and applied at its centre. If the acceleration of the cylinder is

a

and it is rolling without slipping then the value of

F

is:

MEDIUM

Physics>Mechanics>Systems of Particles and Rotational Motion>Moment of Inertia

A solid sphere of mass

M

and radius

R

is divided into two unequal parts. The first part has a mass of

\frac{7 M}{8}

and is converted into uniform disc of radius

2 R

. The second part is converted into a uniform solid sphere. Let

I_{1}

be the moment of inertia of the disc about its axis and

I_{2}

be the moment of inertia of the new sphere about its axis. The ratio

I_{1} / I_{2}

is given by:

MEDIUM

Physics>Mechanics>Systems of Particles and Rotational Motion>Moment of Inertia

From a disc of radius

R

and mass

M

, a circular hole of diameter

R

, whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the centre?

MEDIUM

Physics>Mechanics>Systems of Particles and Rotational Motion>Moment of Inertia

Two identical spherical balls of mass $M$ and radius $R$ each are stuck on two ends of a rod of length $2 R$ and mass $M$ (see figure). The moment of inertia of the system about the axis passing perpendicularly through the centre of the rod is

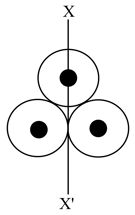
Question Image

MEDIUM

Physics>Mechanics>Systems of Particles and Rotational Motion>Moment of Inertia

A roller is made by joining together two cones at their vertices O. It is kept on two rails AB and CD which are placed asymmetrically (see figure), with its axis perpendicular to CD and its centre O at the centre of line joining AB and CD (see figure). It is given a light push so that it starts rolling with its centre O moving parallel to CD in the direction shown. As it moves, the roller will tend to:

Question Image

EASY

Physics>Mechanics>Systems of Particles and Rotational Motion>Moment of Inertia

Three identical spherical shells, each of mass $m$ and radius $r$ are placed as shown in the figure. Consider an axis $X X^{'}$ which is touching the two shells and passing through the diameter of the third shell. The moment of inertia of the system consisting of these three spherical shells about $X X^{'}$ axis is:

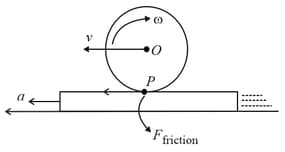
Question Image

MEDIUM

Physics>Mechanics>Systems of Particles and Rotational Motion>Moment of Inertia

A solid sphere and solid cylinder of identical radii approach an incline with the same linear velocity (see figure). Both roll without slipping all throughout. The two climb maximum heights $h_{s p h}$ and $h_{c y l}$ on the incline. The ratio $\frac{h_{s p h}}{h_{c y l}}$ is given by:
Question Image

MEDIUM

Physics>Mechanics>Systems of Particles and Rotational Motion>Moment of Inertia

Consider a cylinder of mass M resting on a rough horizontal rug that is pulled out from under it with acceleration 'a' perpendicular to the axis of the cylinder. What is F_friction at point P ? It is assumed that the cylinder does not slip.
Question Image

HARD

Physics>Mechanics>Systems of Particles and Rotational Motion>Moment of Inertia

A thin circular plate of mass

M

and radius

R

has its density varying as

ρ (r) {=ρ}_{0} r

with

ρ_{0}

as constant and

r

is the distance from its centre. The moment of Inertia of the circular plate about an axis perpendicular to the plate and passing through its edge is

I = a M R^{2}

. The value of the coefficient

a

is:

HARD

Physics>Mechanics>Systems of Particles and Rotational Motion>Moment of Inertia

When a

12000 J

of work is done on a flywheel, its frequency of rotation increases from

10 Hz to 20 Hz

. The moment of inertia of flywheel about its axis of rotation is

(π^{2} = 10)

MEDIUM

Physics>Mechanics>Systems of Particles and Rotational Motion>Moment of Inertia

A thin disc of mass

M

and radius

R

has mass per unit area

σ (r) = k r^{2}

where

r

is the distance from its centre. Its moment inertia about an axis going through its centre of mass and perpendicular to its plane is:

MEDIUM

Physics>Mechanics>Systems of Particles and Rotational Motion>Moment of Inertia

The moment of inertia of a solid sphere, about an axis parallel to its diameter and at a distance of

x

from it, is

I (x) .

Which one of the graphs represents the variation of

I (x)

with

x

correctly?

EASY

Physics>Mechanics>Systems of Particles and Rotational Motion>Moment of Inertia

A thin circular disk is in the

x y

plane as shown in the figure. The ratio of its moment of inertia about

z

and

z'

axes will be:
Question Image

MEDIUM

Physics>Mechanics>Systems of Particles and Rotational Motion>Moment of Inertia

Let the moment of inertia of a hollow cylinder of length

30 cm

(inner radius

10 cm

and outer radius

20 cm

), about its axis be

I

. The radius of a thin cylinder of the same mass such that its moment of inertia about its axis is also

I,

is:

Important Questions on Systems of Particles and Rotational Motion

Learn and Prepare for any exam you want !