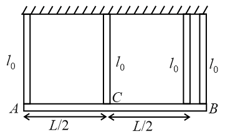
A uniform rod $AB$ of mass $M$ and length $L$ is suspended from four identical wires with two wires at end $B$, one at end $A$ and one at centre. Natural length of wires is ${\ell }_0$. Tensions in wires connected at $A$ is given by $\frac{Mg}{n}$. Find $n$. (Diagram is not drawn to scale)

 

A rod of length $L$ can rotate about end $0 .$ What is the work done if the rod is rotated by $180°$

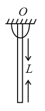
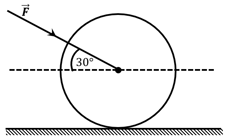
As shown in figure, a $70 \mathrm{kg}$ garden roller is pushed with a force of $\overrightarrow{F}=200 \mathrm{N}$ at an angle of $30°$ with horizontal. The normal reaction on the roller is (Given $g=10 \mathrm{m} {\mathrm{s}}^{-2}$)

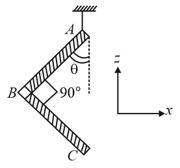
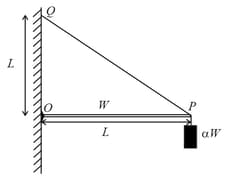
One end of a horizontal uniform beam of weight $W$ and length $L$ is hinged on a vertical wall at point $O$ and its other end is supported by a light inextensible rope. The other end of the rope is fixed at point $Q$, at a height $L$ above the hinge at point $O$. A block of weight $\alpha W$ is attached at the point $P$ of the beam, as shown in the figure (not to scale). The rope can sustain a maximum tension of  $\left(2\sqrt{2}\right)W$. Which of the following statement(s) is(are) correct?

A $\sqrt{34} \mathrm{m}$ long ladder weighing $10 \mathrm{kg}$ leans on a frictionless wall. Its feet rest on the floor $3 \mathrm{m}$ away from the wall as shown in the figure. If $F_f$ and $F_w$ are the reaction forces of the floor and the wall, then ratio of $\frac{F_w}{F_f}$ will be :
(Use $g=10 \mathrm{m} {\mathrm{s}}^{-2}$.)

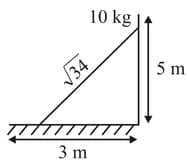
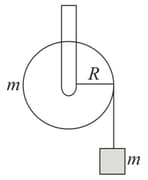
A mass $m$ is supported by a massless string wound around a uniform hollow cylinder of mass $m$ and radius $R$. If the string does not slip on the cylinder, then with what acceleration will the mass release? (Assume $g=$ acceleration due to gravity)

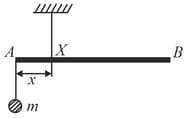
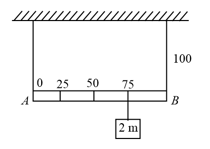
Shown in the figure is rigid and uniform one meter long rod $\mathrm{AB}$ held in horizontal position by two strings tied to its ends and attached to the ceiling. The rod is off mass $\text{'}\mathrm{m}\text{'}$ and has another weight of mass $2 \mathrm{m}$ hung at a distance of $75 \mathrm{cm}$ from $\mathrm{A}$. The tension in the string at $\mathrm{A}$ is:

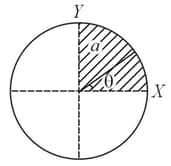
The disc of mass $M$ with uniform surface mass density $\sigma$ is shown in the figure. The centre of mass of the quarter disc (the shaded area) is at the position $\left(\frac{xa}{3\pi }, \frac{xa}{3\pi }\right)$ where $x$ is _______ . (Round off to the Nearest Integer) [$a$ is an area as shown in the figure]

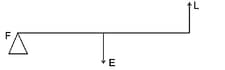
How is it possible to increase the M.A. of the given lever without increasing its length?

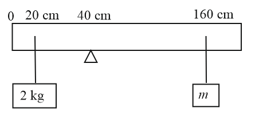
A uniform rod of length $200 \mathrm{cm}$ and mass $500 \mathrm{g}$ is balanced on a wedge placed at $40 \mathrm{cm}$ mark. A mass of $2 \mathrm{kg}$ is suspended from the rod at $20 \mathrm{cm}$ and another unknown mass $m$ is suspended from the rod at $160 \mathrm{cm}$ mark as shown in the figure. Find the value of $m$ such that the rod is in equilibrium. $\left.(g=10 \mathrm{m} {\mathrm{s}}^{-2}\right)$

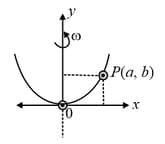
A bead of mass $\mathrm{m}$ stays at point $\mathrm{P}\left(\mathrm{a}, \mathrm{b}\right)$ on a wire bent in the shape of a parabola $y=C{x}^{\mathit{2}}$ and rotating with angular speed $\mathrm{\omega }$ (see figure). The value of $\omega$ is (neglect friction)