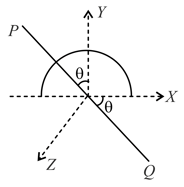
A uniform semicircular disc of mass $2\mathrm{kg}$ and radius $R=2\mathrm{m}$ lies in $x-y$ plane with its centre at origin as shown in figure. Also, axis $PQ$ is in the $x-y$ plane. Then, the moment of inertia (in S.I. unit) of semicircular disc about axis $PQ$ is

 

Two identical small balls $A$ and $B$ are connected at ends of a light rod and placed vertically as shown in figure. Friction is absent everywhere. By small disturbance, the ball $B$ slides away from the wall. Find angle made by the rod with the horizontal, at the moment ball $A$ breaks off from the vertical wall

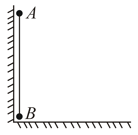
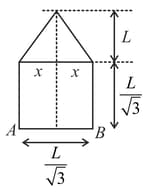
Figure shows a uniform planar object. Height of centre of mass of object from base $AB$ is

A thin uniform rod $AB$ of length $L$ and mass $2.0 \mathrm{kg}$ has a purely translational motion with acceleration $1.0 \mathrm{m} {\mathrm{s}}^{-2}$ under the action of forces $F_1$ and $F_2$. If $F_1=10.0 \mathrm{N}$  and $a=30 \mathrm{cm}$, then the values of $L$ and $F_2$ respectively are

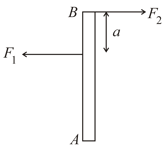
A uniform cube of mass $2.0 \mathrm{kg}$ rests or a rough horizontal surface with coefficient of friction $\mu =0.2$ A force $F$ is applied on the cube as shown. The range of value of $F$ for which the cube will slide without toppling is given by $\left(g=10 \mathrm{m} {\mathrm{s}}^{-2}\right)$

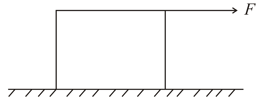
The figure shown is an overhead view of a thin uniform rod of length $L$ and mass $M$ rotating horizontally at angular speed $\omega$ about an axis passing through its centre. A particle of mass $m$ initially attached to the end $A$ is ejected from the rod with velocity $V_p$ which is perpendicular to the rod at the instant of ejection. If $\omega =10.0 \mathrm{rad} {\mathrm{s}}^{-1}, L=1.0m, m=M$ and $V_p$ is $4 \mathrm{m} {\mathrm{s}}^{-1}$ more than the speed of rod end $A$ just after the ejection, then the value of $V_p$ is 

Uniform rod of mass $M$, length $2L$ is suspended with the help of two ideal strings as shown. Complete arrangement is in equilibrium in vertical $x-y$ plane. Find value of $F_0$ so that string $1$ remains vertical (assuming rod is horizontal).

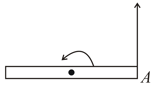
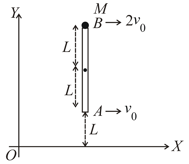
Ends $A$ and $B$ of a rigid uniform rod of mass $M$ parallel to $Y$-axis have velocities ${\overrightarrow{v}}_A=v_0\hat{i},{\overrightarrow{v}}_B=2v_0\hat{i}$ as shown. A point mass $M$ is also attached at the end $B$ of rod, then the angular momentum of system about point $O$ will be

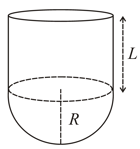
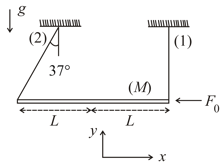
Consider a rigid body which consist of uniform hemispherical shell of radius $R$ and uniform cylindrical shell of height $L$ and radius $R$ (material of hemispherical shell and cylindrical shell are same). Find maximum value of $L$ so that complete rigid body remains in stable equilibrium in the position shown (neglect friction).