Show that the electric field at the surface of a charged conducting sphere is given by E → = σ ε 0 n ^ , where σ is the surface charge density and n ^ is a unit vector normal to the surface in the outward direction.

Let a charge Q be given to a conductor, this charge under electrostatic equilibrium will redistribute and the electric field inside the conductor is zero (i.e., E i n = 0 ). Let us consider a point P at which electric field strength is to be calculated, just outside the surface of the conductor. Let the surface charge density on the surface of the conductor in the neighbourhood of P be σ . Now consider a small cylindrical box CD having one base C passing through P; the other base D lying inside the conductor and the curved surface being perpendicular to the surface of the conductor. Let the area of each flat base be a . As the surface of the conductor is equipotential surface, the electric field strength E at P, just outside the surface of the conductor is perpendicular to the surface of the conductor in the neighbourhood of P. The flux of electric field through the curved surface of the box is zero, since there is no component of electric field E normal to curved surface. Also, the flux of electric field through the base D is zero, as electric field strength inside the conductor is zero. Therefore, the resultant flux of electric field through the entire surface of the box is same as the flux through the face C. This may be analytically seen as: If S 1 and S 2 are flat surfaces at C and D and S 3 is curved surface, then, Total electric flux, ∫ S E → . d S → = ∫ S 1 E → . d S 1 → + ∫ S 2 E → . d S → 2 + ∫ S 3 E → . d S → 3 = ∫ S 1 E . d S 1 cos 0 ∘ + ∫ S 2 0 . d S → 2 + ∫ S 3 E . d S 3 cos 90 ∘ = ∫ S 1 E . d S 1 = E a As the charge enclosed by the cylinder is ( σ a ) coulomb, we have, using Gauss’s theorem, Total electric flux = 1 ∈ ∘ × Charge enclosed Thus, the electric field strength at any point close to the surface of a charged conductor of any shape is equal to 1 ∈ ∘ times the surface charge density σ . This is known as Coulomb’s law. The electric field strength is directed radially away from the conductor if σ is positive and towards the conductor if S is negative. If n ^ is unit vector normal to surface in outward direction, then E → = σ ∈ ∘ n ^ Obviously electric field strength near a plane conductor is twice of the electric field strength near a non-conducting thin sheet of charge.

(i) Express Coulomb's law in vector form. (ii) Two point charges q 1 = 5 × 10 - 6 C and q 2 = 3 × 10 - 6 C are located at ( 3 , 5 , 1 ) m and ( 1 , 3 , 2 ) m . Find F 12 → and F 21 → using vector form of Coulomb's law.

(i) The Coulomb’s law of electrostatic force states that the electrostatic force of attraction and repulsion are directly proportional to the product of the charges and inversely proportional to the square of the distance between the charges. ⇒ F ∝ q 1 × q 2 ⇒ F ∝ 1 r 2 Where, q 1 , q 2 are the charges and r is the distance between the charges Thus, the electrostatic force is given by, ⇒ F = k q 1 q 2 r 2 Where, k is the constant of proportionality The vector form of the Coulomb’s law is given as: F → = k q 1 q 2 r 2 12 r ^ 12 Here, r 12 is the displacement from charge 1 to charge 2. The magnitude of force between charge 1 and charge 2 is equal. But in vector form force on charge 1 is given as: F → 12 = k q 1 q 2 r 2 12 r ^ 12 Force on charge 2 is given as: F → 21 = k q 1 q 2 r 2 21 r ^ 21 ⇒ F → 12 = F → 21 (ii) Here, q 1 = 5 X 10 - 6 C q 2 = 3 X 10 - 6 C r → 2 = ( 3 i ^ + 5 j ^ + k ^ ) r → 1 = ( i ^ + 2 j ^ + 2 k ) ^ r → 12 = r → 2 − r → 1 = ( 2 i ^ + 2 j ^ − k ^ ) r → 12 = ( 2 ) 2 + ( 2 ) 2 + ( - 1 ) 2 = 3 m r ^ 12 = r → 12 r → 12 = 2 i ^ + 2 j ^ - k ^ 3 F → 21 = k q 1 q 2 r 2 12 r ^ 12 = 9 × 10 9 × 5 × 10 - 6 × 3 × 10 - 6 ( 3 ) 2 × 2 i ^ + 2 j ^ - k ^ 3 = 5 × 10 - 3 × ( 2 i ^ + 2 j ^ - k ^ ) N F → 21 = 2 2 + 2 2 + - 1 2 × 5 × 10 - 3 = 1 . 5 × 10 - 2 N As F → 12 = F → 21 = - ( 5 × 10 - 3 ) × ( 2 i ^ + 2 j ^ - k ^ ) N

MEDIUM

NEET

IMPORTANT

Earn 100

A uniformly charged conducting sphere of $2.5 m$ in diameter has a surface charge density of $100 μ C m^{- 2}$ . Calculate the
(i) Charge on the sphere.
(ii) Total electric flux coming out a Gaussian surface just enclosing the outer surface of the sphere.

Important Questions on Electric Charges and Fields

HARD

NEET

IMPORTANT

Gamma Question Bank for Medical Physics>Chapter 16 - Electric Charges and Fields>Assignment>Q 42

A spherical conducing shell of inner radius

r_{1}

and outer radius

r_{2}

has a charge

Q

. Another charge

q

is placed at the centre of the shell.
(a) What is the surface charge density on the
(i) Inner surface?
(ii) Outer surface of the shell?
(b) Derive the expression for the electric field at a point

x > r_{2}

from the centre of the shell.

HARD

NEET

IMPORTANT

Gamma Question Bank for Medical Physics>Chapter 16 - Electric Charges and Fields>Assignment>Q 43

Show that the electric field at the surface of a charged conducting sphere is given by

\vec{E} = \frac{σ}{ε_{0}} \hat{n}

, where

σ

is the surface charge density and

\hat{n}

is a unit vector normal to the surface in the outward direction.

HARD

NEET

IMPORTANT

Gamma Question Bank for Medical Physics>Chapter 16 - Electric Charges and Fields>Assignment>Q 44

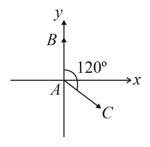
Two small identical electric dipoles $A B$ and $A C$ , each of dipole moment $p$ are kept at an angle of $120 °$ as shown in figure. What is the resultant dipole moment of this combination? If this system is subjected to electric field $(\vec{E})$ directed along $+ x$ direction, what will be the magnitude and direction of torque acting on this?

Question Image

HARD

NEET

IMPORTANT

Gamma Question Bank for Medical Physics>Chapter 16 - Electric Charges and Fields>Assignment>Q 46

(i) State Coulomb's law and write the formula of electrostatic force between two charges, separated by certain distance. Under which condition this formula is applicable?
(ii) Two positive point charges which are

0.1 m

apart repel each other with a force of

18 N

. If the sum of the charges be

9 μ C

, calculate their separate values of charges.

HARD

NEET

IMPORTANT

Gamma Question Bank for Medical Physics>Chapter 16 - Electric Charges and Fields>Assignment>Q 47

(i) Express Coulomb's law in vector form.
(ii) Two point charges

q_{1} = 5 \times 10^{- 6} C

and

q_{2} = 3 \times 10^{- 6} C

are located at

(3, 5, 1) m

and

(1, 3, 2) m

. Find

\vec{F_{12}}

and

\vec{F_{21}}

using vector form of Coulomb's law.

HARD

NEET

IMPORTANT

Gamma Question Bank for Medical Physics>Chapter 16 - Electric Charges and Fields>Assignment>Q 48

(i) Show that path of a charge particle projected normal to an uniform electrostatic field is a parabola.
(ii) A particle of mass

m

and charge

+ q

is thrown at a speed

u

against a uniform electric field

E

. How much distance will it travel before coming to rest?

HARD

NEET

IMPORTANT

Gamma Question Bank for Medical Physics>Chapter 16 - Electric Charges and Fields>Assignment>Q 49

(i) Derive an expression for electric field due to a point charge at a distance

r

from the charge and express it in vector form.
(ii) Four identical point charges of

4 μ C

each are placed at the corners of a square of each side

0.1 m

. Calculate the electric field at the centre of the square.
(iii) Calculate the electric field intensity at the centre, when one of the corner charges is removed.

HARD

NEET

IMPORTANT

Gamma Question Bank for Medical Physics>Chapter 16 - Electric Charges and Fields>Assignment>Q 50

(i) Two charges of a dipole $- 4 μ C$ and $+ 4 μ C$ are placed at the points $A (1, 0, 4) m$ and $B (2, - 1, 5) m$ located in an electric field $\vec{E} = 0.20 \hat{i} V {cm}^{- 1}$ . Calculate the torque acting on the dipole.

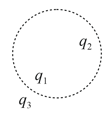
(ii) A Gaussian surface is shown in figure. Charges $q_{1}$ and $q_{2}$ are inside and charge $q_{3}$ is outside the surface. Indicate the charges which contributes the electric field appearing in the formula $\oint \vec{E} \cdot \vec{d s} = \frac{q_{in}}{ε_{0}}$ .

Question Image

(iii) The electric field in a region is given by $\vec{E} = \frac{3}{5} E_{0} \hat{i} + \frac{4}{5} E_{0} \hat{j}$ with $E_{0} = 2 \times 10^{3} {NC}^{- 1} .$ Find the flux of this field through a rectangular surface of area $0.2 m^{2}$ parallel to $y - z$ plane.

A uniformly charged conducting sphere of 2.5 m in diameter has a surface charge density of 100μC m-2. Calculate the (i) Charge on the sphere. (ii) Total electric flux coming out a Gaussian surface just enclosing the outer surface of the sphere.

Important Questions on Electric Charges and Fields

Learn and Prepare for any exam you want !

A uniformly charged conducting sphere of $2.5 m$ in diameter has a surface charge density of $100 μ C m^{- 2}$ . Calculate the
(i) Charge on the sphere.
(ii) Total electric flux coming out a Gaussian surface just enclosing the outer surface of the sphere.