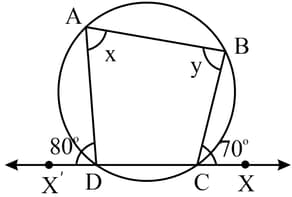
$ABCD$ is a cyclic quadrilateral. If $\angle BCX=70°$ and $\angle AD{X}^{\text{'}}=80°$, then find the values of $x$ and $y$ respectively.

                       

In the given figure, $AEDF$ is a cyclic quadrilateral. The values of $x$ and $y$ respectively are

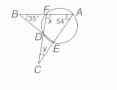
$O$ is the centre of the circle having radius $5 cm$. $AB$ and $AC$ are two chords such that $AB=AC=6 cm$. If $OA$ meets $BC$ at $P$, then $OP=$_____.

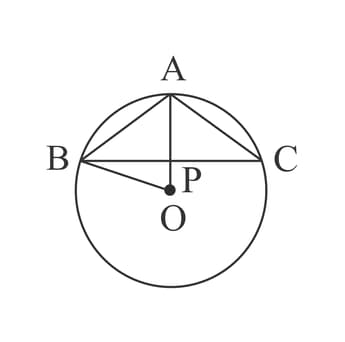
In given figure, if $O$ is the centre of the circle, then $x=$________.

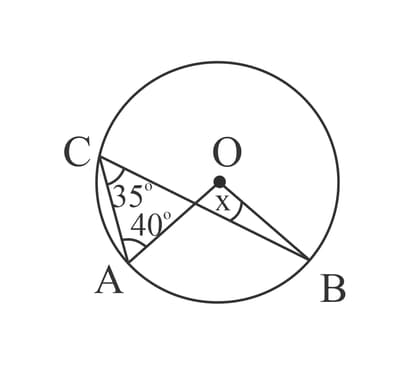
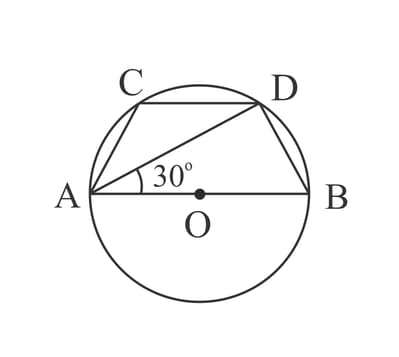
In the given figure, $AOB$ is the diameter of a circle and $CD \mathrm{II} AB$. If $\angle BAD=30°$, then $\angle CAD=$________. 

State 'T' for true and 'F' for false.(Mention the final answer using the given sequence)

(i)A segment of a circle is the region between an arc and radius of the circle.

(ii)The line joining the mid point of a chord to the centre of a circle passes through the mid point of the corresponding minor arc. 

(iii)Angles inscribed in the same arc of a circle are equal.

Two circles intersect at two points $A$ and $B$. If $AD$ and $AC$ are diameters of the circles, then which of the following step is INCORRECT in order to prove that $B$ lies on the line segment $DC$? 

$\left(P\right)$ Join $AB$.

$\left(Q\right)$ $\angle ABD=90°$ and $\angle ABC=90°$ (Angle in semicircle)

$\left(R\right)$ $\angle ABD+\angle ABC=360°$

$\left(S\right)$ $DBC$ is a straight line segment. Hence $B$ lies on the line segment $DC$.