EASY

JEE Main/Advanced

IMPORTANT

Earn 100

An aqueous solution of ${AgNO}_{3}$ is electrolysed using direct current. The electrodes are inert and time dependence of current is represented as

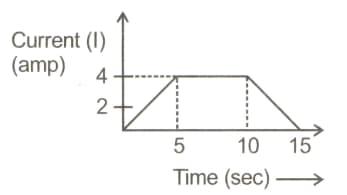
The mass (in $mg$ ) of $Ag (108 g / mol)$ deposited at cathode is [Given $F = 96000 C$ ]

50% studentsanswered this correctly

Important Points to Remember in Chapter -1 - Electrochemistry from Embibe Experts Gamma Question Bank for Engineering Chemistry Solutions

1. Electrochemical Cells:

For any electrode $\to$ Oxidation potential $= -$ Reduction potential.

$E_{c e l l} =$ Reduction potential of cathode $-$ Reduction potential of anode.

$E_{c e l l} =$ Reduction potential of cathode $+$ Oxidation potential of anode.

$E_{c e l l}$ is always a positive quantity for a spontaneous reaction; Anode will be electrode of low reduction potential and Cathode will be of high reduction potential.

${E^{\circ}}_{c e l l} =$ SRP of cathode $-$ SRP of anode. (SRP = Standard Reduction Potential)

The greater is the SRP value, the greater will be oxidising power.

2. Different types of Electrodes:

(i) Metal-metal ion electrode $(M^{+ n} | M)$

$M^{n +} + {n e}^{-} \to M (s)$

(ii) Gas-ion Electrode $P t |H_{2} (P a t m)| H^{+} (X M)$

As reduction electrode $, H^{+} (a q) + e^{-} \to \frac{1}{2} H_{2} (P a t m), E = E^{°} - 0.0591 l o g \frac{P_{H_{2}}^{\frac{1}{2}}}{[H^{+}]}$

(iii) Oxidation-reduction electrode $P t | {F e}^{2 +}, {F e}^{3 +}$

As reduction electrode, ${F e}^{3 +} + e^{-} ⟶ {F e}^{2 +} E = E^{\circ} - 0.0591 \log \frac{[{F e}^{2 +}]}{[{F e}^{3 +}]}$

(iv) Metal-metal insoluble salt electrode $e . g ., A g | A g C l, {C l}^{-}$

As reduction electrode, $A g C l (s) + e^{-} ⟶ A g (s) + {C l}^{-}$ .

$E_{{C l}^{-} |A g C l| A g} = E_{{C l}^{-} |A g C l| A g}^{0} - 0.0591 \log [{C l}^{-}]$

3. Gibbs Free Energy Change:

$Δ G = - n F E_{c e l l}$

4. Nernst Equation:

(Effect of concentration and temperature on emf of cell)

$Δ G = Δ G^{°} + R T l n Q$ (where $Q$ is reaction quotient)

$Δ G^{°} = - R T l n K_{e q}$

$E_{c e l l} = {E^{\circ}}_{c e l l} - \frac{2.303 R T}{n F} l o g Q$

$E_{c e l l} = {E^{\circ}}_{c e l l} - \frac{0.0591}{n} l o g Q [A t 298 K]$

At chemical equilibrium: $Δ G = 0$ ; $E_{c e l l} = 0$

$l o g K_{e q} = \frac{n E_{c e l l}^{0}}{0.0591}$

$E_{c e l l}^{0} = \frac{0.0591}{n} l o g K_{e q}$

5. Concentration Cell:

A cell in which both the electrodes are made up of the same material.

For all concentration cell,

${E^{\circ}}_{c e l l} = 0$

(i) Electrolyte Concentration Cell:

$e . g ., Z n (s) | {Z n}^{2 +} (c_{1}) ‖ {Z n}^{2 +} (c_{2}) | Z n (s) E = \frac{0.0591}{2} l o g \frac{C_{2}}{C_{1}}$

(ii) Electrode Concentration Cell:

e.g., $P t, H_{2} (P_{1} a t m) | H^{+} (1 M) | H_{2} (P_{2} a t m) | P t E = \frac{0.0591}{2} l o g (\frac{P_{1}}{P_{2}})$

6. Calculation of different Thermodynamics Function of Cell Reaction:

$Δ G = - n F E_{c e l l}$

$∆ S = - {[\frac{d G}{d T}]}_{P}$ (At constant pressure)

$Δ S = - {[\frac{d (Δ G)}{d T}]}_{P} = n F {(\frac{d}{d t} (E_{c e l l}))}_{P}$

${[\frac{\partial E}{\partial T}]}_{P} =$ Temperature coefficient of emf of the cell.

$Δ H = n F [T {(\frac{\partial E}{\partial T})}_{P} - E]$

$Δ C p$ of cell reaction:

$C_{P} = \frac{d H}{dT}$

$Δ C_{P} = \frac{d}{d T} (Δ H)$

$Δ C_{P} = n F T \frac{d^{2} E_{c e l l}}{d T^{2}}$

7. Electrolysis:

(i) $\frac{K^{+}, {C a}^{+ 2}, {N a}^{+}, {M g}^{+ 2}, {A l}^{+ 3}, {Z n}^{+ 2}, {F e}^{+ 2}, H^{+}, {C u}^{+ 2}, {A g}^{+}, {A u}^{+ 3}}{I n c r e a s i n g o r d e r o f d e p o s i t i o n .} >$

(ii) Similarly, the anion which is stronger reducing agent (low value of $S R P$ ) is liberated first at the Anode.

$\frac{{S O}_{4}^{2 -}, {N O}_{3}^{-}, {O H}^{-}, {C l}^{-}, {B r}^{-}, I^{-}}{I n c r e a s i n g o r d e r o f d e p o s i t i o n} >$

8. Faraday's Law of Electrolysis:

(i) First Law:

$w = Z q w = Z i t$ Where $Z =$ Electrochemical equivalent of substance.

(ii) Second Law:

$W α E or \frac{W}{E} = c o n s t a n t \frac{W_{1}}{E_{1}} = \frac{W_{2}}{E_{2}}$

$\frac{W}{E} = \frac{i \times t \times c u r r e n t e f f i c i e n c y f a c t o r}{96500}$

$C u r r e n t e f f i c i e n c y = \frac{A c t u a l m a s s deposited / produced}{T h e o r e t i c a l m a s s deposited / produced} \times 100$

9. Conductance in Electrolytic Solutions:

(i) $C o n d u c t a n c e = \frac{1}{R e s i s t a n c e}$

(ii) Specific conductance or conductivity:

(Reciprocal of specific resistance) $κ = \frac{1}{ρ} κ =$ specific conductance

specific conductance $=$ conductance $\times \frac{l}{a}$

(iii) Equivalent conductance:

$Λ_{E} = \frac{κ \times 1000}{Normality} unit : {ohm}^{- 1} {cm}^{2} {eq}^{- 1}$

(iv) Molar conductance:

$Λ_{m} = \frac{κ \times 1000}{Molarity} unit : {ohm}^{- 1} {cm}^{2} {mole}^{- 1}$

10. Kohlrausch's Law:

Variation of $λ_{e q} & λ_{M}$ of a solution with concentration:

(i) Strong electrolyte $λ_{M}^{c} = λ_{M}^{\infty} - b \sqrt{c}$

(ii) For both strong and weak electrolytes:

$λ_{\infty} = n_{+} λ_{+}^{\infty} + n_{-} λ^{\infty}$ where $λ$ is the molar conductivity.

$n_{+} =$ No. of cations obtained after dissociation per formula unit.

$n_{-} =$ No. of anions obtained after dissociation per formula unit.

11. Application of Kohlrausch’s Law:

(i) Calculation of $λ_{m}^{0}$ of weak electrolytes:

$λ_{M ({C H}_{3} C O O H)}^{o} = λ_{M ({C H}_{3} C O O N a)}^{0} + λ_{M_{(H C l)}}^{0} - λ_{M (N a C l)}^{0}$

(ii) To calculate degree of dissociation of a weak electrolyte

$α = \frac{λ_{m}^{}}{λ_{m}^{0}}; K_{e q} = \frac{c α^{2}}{(1 - α)}$

(iii) Solubility $(S)$ of sparingly soluble salt & their $K_{s p}$

$λ_{M} = λ_{M}^{o} = κ \times \frac{1000}{s o l u b i l i t y} K_{s p} = S^{2}$

(iv) Ionic mobility: It is the distance travelled by the ion per second under the potential gradient of $1$ volts per $c m$ . Its unit is ${c m}^{2} s^{- 1} v^{- 1}$ .

(v) Absolute ionic mobility:

$λ_{c}^{o} {α μ}_{c}; λ_{a}^{0} \propto μ_{a}$

$λ_{c}^{0} = F \times μ_{c}^{0}; λ_{a}^{0} = F \times μ_{a}^{0}$

$I o n i c M o b i t i t y μ = \frac{S p e e d}{P o t e n t i a l g r a d i e n t} = \frac{v}{\frac{V}{l}}$

(vi) Transport Number:

$t_{c} = [\frac{μ_{c}}{μ_{c} + μ_{a}}], t_{a} = [\frac{μ_{a}}{μ_{a} + μ_{c}}]$

Where $t_{c} =$ Transport Number of cation & $t_{a} =$ Transport Number of anions.

An aqueous solution of AgNO3 is electrolysed using direct current. The electrodes are inert and time dependence of current is represented as The mass (in mg ) of Ag108 g/mol deposited at cathode is [Given F=96000C ]

Important Points to Remember in Chapter -1 - Electrochemistry from Embibe Experts Gamma Question Bank for Engineering Chemistry Solutions

Learn and Prepare for any exam you want !

An aqueous solution of ${AgNO}_{3}$ is electrolysed using direct current. The electrodes are inert and time dependence of current is represented as

The mass (in $mg$ ) of $Ag (108 g / mol)$ deposited at cathode is [Given $F = 96000 C$ ]